Un tetraedro regular es una pirámide que consiste de cuatro triángulos equiláteros, cada uno de ellos unido al los otros tres a lo largo de sus lados. Dando por resultado seis orillas, y en consecuencia, todos tienen el mismo largo. Imagine que en cada una de los quatro caras, un automóvil viaja en la dirección del reloj a una velocidad constante a lo largo de las orillas que limitan esa cara. Cada uno de los quatro automóviles puede estar viajando a diferente velocidad y puede empezar en cualquier parte de su cara fronteriza. ![]() Pueden los automóviles siempre evitar un choque, o están destinados a un accidente a lo largo de alguna orilla?
Pueden los automóviles siempre evitar un choque, o están destinados a un accidente a lo largo de alguna orilla?
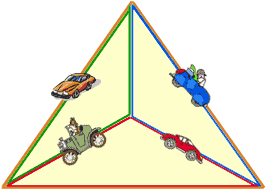
Recibimos soluciones similares de Juan Mir Pieras (España) y Alexander Potapenko (Rusia.) Empezaremos con la solución de Potapenko.
Ni siquiera tres automóviles pueden evitar una colisión. Denotemos los vértices del tetraedro con las letras A, B, C, D. Entonces, como se muestra en el diagrama, tres automóviles viajarán las trayectorias ABC, ADB, BCD respectivamente.
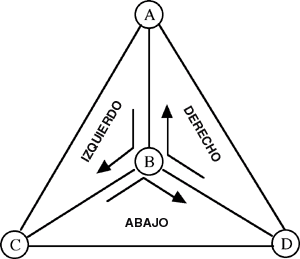
Uno de los automóviles tendrá la velocidad mínima. (Si 2 o 3 automóviles tienen la velocidad mínima tome cualquiera de ellos.) Sea éste automóvil ABAJO. Examinemos el momento en que este automóvil se localiza en B (y viaja hacia D.)
![]() Dónde puede el automóvil DERECHO estar localizado? Por supuesto que no puede estar en BD, porque la colisión es inevitable con el automóvil ABAJO.
Dónde puede el automóvil DERECHO estar localizado? Por supuesto que no puede estar en BD, porque la colisión es inevitable con el automóvil ABAJO.
No puede estar en AD tampoco Ð porque por su velocidad mayor alcanzaría a D antes (o al mismo tiempo) que el automóvil ABAJO y una colisión con BD sería inevitable.
Similarmente podemos probar que el automóvil IZQUIERDO no puede estar en BC o AC. La forma más fácil de hacerlo Ð recorra el diagrama en forma contraria. Si un movimiento hacia adelante se recorre sin colisiones, entonces el diagrama recorrido al contrario por la misma razón será sin colisiones. Para el automóvil ABAJO con movimiento al contrario, el automóvil IZQUIERDO toma el lugar del automóvil DERECHO moviéndose hacia adelante, así que las posiciones BC y AC están prohibidas.
Vemos así que para que ambos automóviles IZQUIERDO y DRECHO puedan evitar una colisión con el automóvil ABAJO, ellos deben de estar en AB y una colisión entre ellos es inevitable. (Note que no importa cuál de ellos llega primero a AB Ð la colisión será en un futuro cercano o se sucedió en un pasado reciente.) Esto prueba completamente que con cualquiera de los tres automóviles una colisión es inevitable.
ComentariosA pesar de que el argumento matemático de arriba es convincente, una abogado hábil aun podría argüir el caso de que hay una forma de evitar colisiones: si todos los automóviles se movieran a velocidad cero no habría colisiones en absoluto. En efecto, este parece ser una buena forma de eliminar los problemas del tráfico mundial Ð hacer justamente una ley para que todo mundo esté obligado a tener su automóvil estacionado todo el día. Por otra parte, las dos soluciones recibidas incluyen sugerencias de versiones modificadas del problema que permite formas no triviales de evitar colisiones.
Potapenko observó que hay dos automóviles, por ejemplo ABC y ADB, que viajan en la dirección del reloj, y dos, BCD y ADC, que viajan en dirección contraria a la dirección del reloj, entonces pueden fácilmente arreglarse los automóviles para que se eviten uno al otro. Con estas nuevas direcciones de movimiento y la misma velocidad para todos los cuatro automóviles, tenemos dos parejas independientes en conflicto (donde la misma dirección es un conflicto.) Automóviles en pareja pueden moverse por una regla simple: cuando un automóvil está en la mitad de una arista común el otro está en el vértice opuesto. En efecto, en Italia automovilistas usan su propia versión de esta solución con frecuencia ellos manejan en el sentido opuesto de la dirección de la calle y ocasionalmente manejan en sentido opuesto al de las calles de un solo sentido (a alta velocidad) justamente para evitar colisiones. Ellos también manejan sus automóviles en las aceras, posiblemente por la misma razón.
La solución de Mir hace uso de modelos explícitos. Una buena consecuencia de este método es la generalización natural de este problema que permite a los automóviles pasarse en un vértice. (Personalmente a mi no me gustaría estar en uno de los automóviles que llega a una intersección al mismo tiempo que un automóvil que llega desde el otro lado; sin embargo, esto es matemáticas, no física, así que nos permitimos investigar una modificación del problema si lo deseamos.) Con tres automóviles moviéndose a la misma velocidad y uno moviéndose exactamente a la mitad de ésta, hay una solución. Una forma fácil de describirla es enumerando las aristas del 1 al 6 como en la figura.
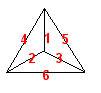
Para la solución mostramos la arista transcurrida por el automóvil correspondiente durante la unidad de tiempo dada.
| IZQUIERDO | ... | 1 | 2 | 4 | 1 | 2 | 4 | ... |
| DERCHO | ... | 5 | 3 | 1 | 5 | 3 | 1 | ... |
| ABAJO | ... | 3 | 6 | 2 | 3 | 6 | 2 | ... |
| ATRAS | ... | 4 | 4 | 6 | 6 | 5 | 5 | ... |
Observe que ninguna columna tiene un número de una arista repetido, lo cual interpretamos como diciéndonos que ninguna pareja de automóviles de los cuatro está en la misma arista al mismo tiempo. Note, sin embargo, que cada uno de los automóviles se llega a juntar con un automóvil en un vértice de acuerdo con la solución del problema original. Mir prueba que una solución es del mismo modo posible cuando hay un automóvil rápido y tres viajan a la mitad de su velocidad, pero no otra combinación de velocidades admite una solución de esta generalización del problema.
El origen de nuestro problema de febrero fue el número 130 del problema de la semana de la página web de Alberto Delgado de la Universidad de Bradley (Peoria, IL): http://bradley.bradley.edu/~delgado/potw/potw.html Quien a su vez lo recibió de su colega, Tony Bedenikovic. El profesor Delgado amablemente nos proveyó del siguiente antecedente.
El problema en realidad se deriva de un problema mas profundo resuelto por Antón A. Klyachko en Comunications in Álgebra, 21 (7), 1993. Aquí, Klyachko prueba que debe de haber por lo menos dos puntos en el tetraedro donde la colisión ocurre. Aún más general, no necesitamos restringirnos a tetraedros. Tenemos un resultado similar para cualquier partición de una 2-esfera en dominios simplemente conectados. Klyachko usa este hecho "simple" para probar un resultado muy profundo en teoría de grupos.