Esta es la solución que recibimos de Juan Pieras de España. Esta generaliza el argumento de la primera solución que se encuentra en nuestra página en Inglés cuando se tienen 2n clientes formados en la fila. También en la página de Inglés se muestra otra solución differente la cual usa el principio de reflección.
Mi respuesta a la pregunta de este mes es:
Si llegan cuatro personas con una moneda de un dólar y cuatro con una moneda de dos, y se colocan al azar en la cola de una ventanilla para un espectáculo que cuesta un dólar, y en el que la cajera inicialmente no tiene cambio, la probabilidad de que en ningún momento tenga problema para devolver cambio es 1/5.
Lo que voy a tratar de demostrar es que si llegan n personas con una moneda de un dólar y n con una moneda de dos, esa probabilidad vale 1/(n+1).
La pregunta de este mes sería, pues, el caso particular para n=4.
Para empezar la demostración, me centraré en el siguiente esquema, en el que quedan dibujadas todas las ordenaciones de llegada posibles. Empezando desde el punto blanco, en el que la cajera no tiene cambio, las flechas verdes indican que llega una persona con una moneda de un dólar, y las azules que llega una persona con una moneda de dos dólares. Así, todos los caminos posibles entre el punto blanco inicial y el punto negro final contienen n flechas verdes y n azules.
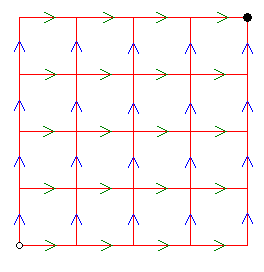
Los caminos que son solución del problema son los que se dibujan en el siguiente esquema, ya que la diagonal del cuadrado grande n·n marca cambio=0 (las "diagonales" paralelas marcan las diferentes situaciones del cambio que posee la cajera).
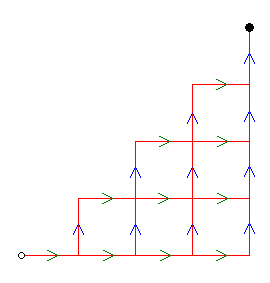
Mi solución intenta buscar una recursividad, pero con los esquemas anteriores no es suficiente, así que ahora voy a dibujar los esquemas correspondientes a la siguiente situación: la cajera dispone inicialmente de h monedas de dólar, y van llegando, ordenadas al azar, n personas con una moneda de dólar y n+h con una moneda de dos dólares. Hay que notar que el caso del problema inicial es simplemente un caso particular de éste, para h=0.
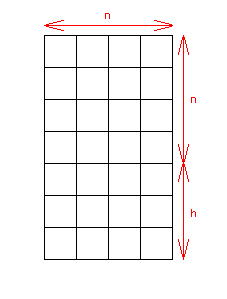
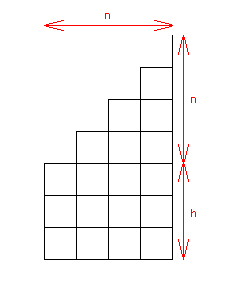
Voy a llamar cp(n,h) al número de caminos posibles del punto inicial al final.
Estudiando la primera bifurcación, se ve que se cumple la siguiente ley recursiva:
Si n=0, cp(0,h)=1
Si n>0 y h=0, cp(n,0)=2·cp(n-1,1)
Si n>0 y h>0, cp(n,h)=cp(n-1,h+1)+cp(n,h-1)
De manera similar, voy a llamar cf(n,h) al número de caminos favorables.
Estudiando la primera bifurcación, se ve que se cumple la siguiente ley recursiva:
Si n=0, cf(0,h)=1
Si n>0 y h=0, cf(n,0)=cf(n-1,1)
Si n>0 y h>0, cf(n,h)=cf(n-1,h+1)+cf(n,h-1)
Puede verse que cp y cf tienen expresiones muy similares, y que cf(n,h)<=cp(n,h).
Si hacemos una tabla para los primeros valores de cp, cf y cd=cp-cf, y lo comparamos con el triángulo de Tartaglia donde comb(i,j)=i!/(j!·(i-j)!), podemos conjeturar que:
A) cp(n,h)=comb(2n+h,n)
B) cd(n>0,h)=comb(2n+h,n-1), cd(0,h)=0
Operando A y B, obtendríamos que entonces
C) cf(n,h)=comb(2n+h,n)·(h+1)/(n+h+1)
Se puede ver que las conjeturas A y C son ciertas, ya que cumplen las leyes recursivas que hemos enunciado antes.
La probabilidad p(n,h) de que la cajera se quede sin cambio, es entonces
p(n,h)=cf(n,h)/cp(n,h)=(h+1)/(n+h+1)
Para el caso del problema inicial,
p(n)=p(n,0)=1/(n+1)
p(4)=1/5
Querría acabar con una pregunta. La afirmación A podría haberse hecho desde el principio desde un punto de vista de combinatoria, ya que hay tantos caminos posibles como maneras de ordenar a n personas con una moneda de dólar de entre n+(n+h) que llegan a la cola. ¿Tiene también la afirmación B una explicación desde el punto de vista combinatorio?