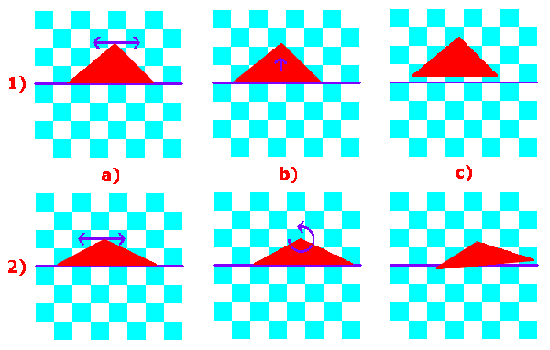
Dado un triánglulo y un tablero infinito con cuadros azules y blancos, demuestre que el triángulo puede ser puesto en el tablero con todos sus vertices strictamente en los cuadros azules.
Solución de MP33
Recibimos soluciones correctas de Pierre Bornsztein (Francia),
Patrick J. LoPresti (Estados Unidos), y Juan Mir Pieras (España.)
Encontramos el problema en Siam Review 13:1 (Enero 1971), p. 115; 14:4
(Octubre 1972), p. 647 D.J. Newman (Yeshiva University) ambos proponen
el problema y
dan su
solución. Una solución no es muy difícil; lo que es
difícil es escribirla. Mir evitó esta dificultad dando su solución
en gráficas.
Primero, la solución en una combinación de palabras
de Bornsztein y Newman.
Supongamos que las celdas del tablero de ajedrez son cuadrados unitarios, orientados de tal manera que sus lados son horizontales y verticales. (Si lo prefiere, puede introducir coordinadas de tal manera que las esquinas de los cuadros son aquellos puntos con dos coordenadas dadas por números enteros.) Ponga un vértice A de nuestro triángulo ABC en una esquina de uno de los cuadros, y gírelo de manera que
- ningún vértice esta en un lado de los cuadros, y
- la longitud de las proyecciones ortogonales en las líneas verticales y horizontales del tablero no son números enteros.
Ahora, traslade el triángulo horizontalmente hasta que B esté en una línea vertical. Nuestro giro inicial asegura que ni A o B están en una esquina de un cuadro, mientras que C esta en el interior de un cuadro. Por lo tanto, un pequeño movimiento ya sea horizontal o vertical no cambia el color de C, pero pueden independientemente intercambiarse los colores de los otros dos vértices. Entonces, uno obtiene fácilmente tres vértices en el interior de cuadros del mismo color. Si el color es azul, entonces nuestro trabajo esta terminado; si es blanco, traslade el triángulo una unidad hacia arriba.
Lo Presti empezó en forma diferente. Él hizo uso del hecho de que todos los puntos a lo largo de una diagonal de los cuados azules son azules excepto en las esquinas. Si deslizamos el lado AB a lo largo de una diagonal azul, entonces habrá una posición donde C yace dentro de un cuadro azul excepto en el molesto caso donde C se mueve a lo largo de una diagonal blanca. No es demasiado difícil esquivar este caso.
Finalmente, este es le argumento de Mir.
Note que es similar en esencia a nuestro argumento verbal, pero requiere dos casos.