Aquí esta otro problema de dados para la temporada de vacaciones. Con un par ordinario de dados la distribución de la suma es
| Sumas posibles | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Distribución de las sumas | 1 | 2 | 3 | 4 | 5 | 6 | 5 | 4 | 3 | 2 | 1 |
La tabla nos dice que la suma 2 aparece en mas de una forma (como 1 + 1), 3 aparece en dos formas (como 1 + 2 y como 2 + 1), y así sucesivamente. El problema para enero es encontrar otra forma de poner números en los dados que den la misma distribución de las sumas.
Solución de MP38Agradecemos a Ed Doolittle de la Universidad de Regina por sugerir nuestro problema de enero. Lo encontró en A Problem Seminar, de Donald J. Newman (Problem Books in Mathematics, 1982), páginas 18 y 98-99. Soluciones completas fueron enviadas por Gilles Feyrit (Francia), Wolfgang Kais (Alemania), Normand Laliberté (Ontario), y Patrick LoPresti (Estados Unidos). Los últimos tres enviaron soluciones similares, cada una con buenas ideas que combinadas forman una solución realmente buena. Feyrit tomó una dirección diferente: él usó polinomios. En añadidura recibimos de Andreas Schüller (Alemania) una buena forma de describir una de las dos familias infinitas de soluciones.
Empezaremos con la estrategia directa.
I. La solución combinada de Kais, LaLiberté, y LoPresti, con una idea de Schüller.
Nuestro problema es diseñar un par de dados con la misma distribución de sumas que un dado común. Específicamente, queremos que las sumas que se muestran en la hilera superior de la tabla se sucedan el mismo número de veces que el mostrado en la hilara inferior.
| Sumas posibles | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Frecuencia deseada | 1 | 2 | 3 | 4 | 5 | 6 | 5 | 4 | 3 | 2 | 1 |
A pesar de que no lo pedimos explícitamente, mas vale que supongamos que los números en las caras de nuestro dado se representen por puntos, y por lo tanto son enteros positivos. Podríamos también permitir fracciones o números negativos, pero
Observación. Si un par de dados da una solución a nuestro problema, entonces también la da un segundo par obtenido del primero al añadirle un número fijo x a cada cara de uno de los dados y substrayendo x de cada cara de su pareja.
En otras palabras, cualquier solución particular a nuestro problema nos lleva a soluciones infinitas. Como consecuencia, si el número más pequeño que aparece en un dado es d, entonces añadimos x = 1 – d a cada cara y la cara más pequeña mostrará el número 1. Veremos que hay dos soluciones básicas donde la cara más pequeña es un 1.
Colorearemos el dado rojo y verde, y marcaremos sus caras en el orden r1 ≤ r2 ≤ ... ≤ r6, y g1 ≤ g2 ≤ ... ≤ g6. Para nuestra solución básica estaremos de acuerdo en que r1 = 1. Ya que la suma más pequeña es 2, inmediatamente también obtenemos g1 = 1. Ya que una suma de 2 se sucede solamente una vez, debemos tener ambos
r2 > 1 and g2 > 1;
una razón similar en el extremo final muestra que para tener una suma más grande que 12 = r6 + g6, debemos de tener
r5 < r6 and g5 < g6.
Para que la suma 3 se suceda dos veces debemos tener dos 2ces, ya sea con un 2 en cada dado o ambos 2ces en un dado. Consideramos los casos separadamente.
Caso 1. Supongamos que r2 = g2 = 2.
Para que la suma de 4 se suceda tres veces en el mismo caso, necesitamos dos 3ces (porque ya tenemos un 4 con 2+2). Estos podrían ambos ser en un dado, digamos el rojo, o podría haber un 3 en ambos dados. No eliminaremos la primera posibilidad.
Posibilidad 1a: r3 = r4 = 3. Nuestras hipótesis nos dejan en este punto con la posibilidad
| Dado rojo | 1 | 2 | 3 | 3 | r5 | r6 |
| Dado verde | 1 | 2 | g3 | g4 | g5 | g6 |
Ahora tenemos dos sumas de 5 y necesitamos dos mas (lo que significa que necesitamos dos 4s), y ninguna suma de 6 (porque bajo nuestra hipótesis actual podríamos no usar 3+3), así que necesitamos cinco mas (lo que significa que se necesitan tres 5s junto con dos 4s). Para nuestros dos 4s, porque r5 < r6 ambos no pueden estar en el dado rojo; por la misma razón no podemos tener dos 5s rojos, ni podemos tener dos 4s verdes con dos 5s verdes. Entonces, uno de los 4s va para cada dado.
Aún mas, no podemos entonces tener tres 5s verdes (esto haría g5 = g6). Estamos forzados a tener un 4 rojo y otro verde, y dos 5s verdes y uno rojo:
| Dado rojo | 1 | 2 | 3 | 3 | 4 | 5 |
| Dado verde | 1 | 2 | 4 | 5 | 5 | g6 |
Para hacer la suma lo más grande que un 12, ahora estamos forzados a poner g6 = 7. Desafortunadamente ahora hay el número equivocado de muchas sumas. (Por ejemplo, hay solamente un 11 en lugar de dos.) Concluimos que la posibilidad primera nos es posible después de todo: no podemos tener ambos 3ces en un dado. Debemos tener
Posibilidad 1b: r3 = g3 = 3. Entonces caso 1 definitivamente se ve como esto:
| Dado rojo | 1 | 2 | 3 | r4 | r5 | r6 |
| Dado verde | 1 | 2 | 3 | g4 | g5 | g6 |
Podemos continuar en esta forma para eliminar la posibilidad de que ambos 4s estén un dado (digamos (1, 2, 3, 4, 4, r6)), y finalmente concluir que
En el caso 1 podemos tener solamente un dado común
Hay una estrategia mejor, usando una sugerencia de Gilles Feyrit. Su idea esta basada en un principio importante para resolver un problema:
Siempre busque la simetría y la forma de aprovecharla.
En nuestro problema la distribución de sumas es simétrica con respecto al valor central de 7. Esto obliga a cada dado a ser simétrico con respecto a su valor promedio de tal manera que una suma de s arriba del promedio se sucede tan frecuentemente como la suma s del promedio de abajo. Entonces, simetría aquí significa que
(promedio de r3 y r4) = (promedio de r2 y r5) = (promedio de r1 y r6) = (promedio del dado rojo),
con una afirmación similar para el promedio verde. Aún mas, las suma del promedio rojo mas el promedio verde deben de ser 7. (Por supuesto, uno debe probar tales afirmaciones, pero aquí la demostración es sin complicaciones; la dejaremos a la imaginación del lector.)
Re-examinemos la primera posibilidad, esta vez usando simetría. Recuerde que habíamos supuesto que había dos 3ces en el dado rojo: (1, 2, 3, 3, r5, r6). La simetría obliga al promedio del valor rojo a ser (r3+r4)/2 = (3+3)/2 = 3, así que sus caras restantes necesariamente serían r5 = (promedio + 1) = 4 (ya que r2 = (promedio – 1)), y r6 = (promedio + 2) = 5 (ya que r1 = (ave – 2)). Entonces el dado verde (1, 2, g3, g4, g5, gl) sería g3 = 4 (para obtener el número correcto de sumas del 5), y g4 = 4 (para que el promedio verde sea 4). Pero ya vimos que en este punto el 5 aparece muy frecuentemente como una suma, de inmediato tenemos una contradicción. Concluimos rápidamente que teniendo ambos 3ces en un dado no es posible. Estamos ciertos por lo tanto que en este caso 1 (con un 2 en ambos dados) 1, 2, y 3 deben aparece en ambos dados. Para obtener los números correctos de 5s por lo menos un dado necesitaría un 4, digamos r4 = 4. Simetría ahora lo arregla todo! El promedio en le dado rojo es necesariamente (r3+r4)/2 = (3+4)/2 = 3.5, de modo que necesariamente sería el promedio en le otro dado (para obtener un promedio de suma del 7), y de modo que nos quedamos con un par común de dados.
Caso 2. Ambos 2ces están en el mismo dado.
Pongámoslos en el dado rojo, lo cual es entonces (1, 2, 2, r4, r5, r6). No podemos usar ahora 2 + 2, así que para obtener una suma de 4 tres veces necesitamos tres 3ces. Estos no pueden estar todos en le dado verde, porque habría entonces demasiados 5s. Así que r4 = 3 y el promedio en le dado rojo debe ser (r3+r4)/2 = (2+3)/2 = 2.5. El dado rojo es por lo tanto (usando simetría)
(1, 2, 2, 3, 3, 4).
El dado verde debe tener un tercer 3, entonces g2 = 3. Necesitamos una suma mas de 5, sea g3 = 4. Porque 2.5 + (promedio verde) = 7, debemos tener (g3+g4)/2 = 4.5; por lo tanto, g4 = 5. El dado verde debe por lo tanto verse como
(1, 3, 4, 5, 6, 8).
En este punto sabemos solamente que el dado debe verse como éste si hay esperanza de tener ambos 2ces en el mismo dado. Debemos ahora comprobar que la distribución que nos esta obligada resulta ser la correcta. Por nuestra construcción ya sabemos que las sumas de 2, 3, 4, y 5 se suceden en el número correcto de veces. Por la simetría resta comprobar solamente que las sumas de 6 y 7 tienen la frecuencia correcta. Por buena suerte, lo son! Haciendo una lista de sumas con el valor rojo primero tenemos
6 = 1+5, 2+4, 2+4, 3+3, 3+3, (son cinco sumas de 6);
7 = 1+6, 2+5, 2+5, 3+4, 3+4, 4+3, (son seis sumas de 7).
Nuestra gran conclusión: Hay dos clases de soluciones, caso 1 (el dado común)
rojo = (1, 2, 3, 4, 5, 6) y verde = (1, 2, 3, 4, 5, 6),
y el caso 2 (el dado nuevo y extraño)
rojo = (1, 2, 2, 3, 3, 4) y verde = (1, 3, 4, 5, 6, 8).
De querer permitir dados con caras en blanco, tenemos tres posibilidades mas:
| Rojo | Verde | |
| Del caso 1 | (0, 1, 2, 3, 4, 5) | (2, 3, 4, 5, 6, 7) |
| Del caso 2 | (0, 1, 1, 2, 2, 3) | (2, 4, 5, 6, 7, 9) |
| (2, 3, 3, 4, 4, 5) | (0, 2, 3, 4, 5, 7) |
Finalmente, si desea permitir números reales arbitrarios en las caras, puede obtener mas ejemplos al añadir el mismo número a cada cara de un dado en la solución básica, y substraer ese mismo número de cada cara del otro.
II. Solución de Gilles Feyrit Funciones generadas.
El punto de partida para esta estrategia es la observación de que los números en las caras de un par de dados se suman como los exponentes de polinomios bajo multiplicación. En efecto, en combinatoria es comúnmente útil reducir un problema que requiere contar combinaciones a un problema de factorización de polinomios. Estos polinomios se llaman funciones generadas. La idea aquí es simple: el dado rojo con sus caras numeradas r1 ≤ r2 ≤ ... ≤ r6 es representada por el polinomio r = xr1+xr2+...+xr6 = ; el dado verde con sus caras g1 ≤ g2 ≤ ... ≤ g6, por el polinomio g = xg1+xg2+...+xg6. Para el dado común los polinomios correspondientes son iguales uno al otro,
r = g = x + x2 + x3 + x4 + x5 + x6.
Cuando los multiplicamos, los coeficientes que aparecen en el producto son fácilmente reconocidos como los que dan la distribución del resultado de tirar un par de dados:
r·g = x2 + 2x3 + 3x4 + 4x5 + 5x6 + 6x7 + 5x8 + 4x9 + 3x10 + 2x11 + x12
Observe, por ejemplo, el coeficiente 4 de x9 corresponde al hecho de que un resultado de 9 se sucede en cuatro formas cuando los dados son arrojados.
Nuestra meta es encontrar polinomios diferentes r* y g* cuyos coeficientes suman 6 (porque cada dado tiene 6 caras), y cuyo producto es r*·g* = r·g. (Observación: para obtener la suma de los coeficientes nada mas hacemos x = 1 en el polinomio.) Como consecuencia, debemos encontrar los factores de r y g que tienen coeficientes enteros. Aquí Feyrit usó número complejos para determinar los factores posibles. Alternativamente, si sabe que
1 + x + x2 + x3 +
x4 + x5 = ![]()
entonces la tarea es fácil: r =
g = ![]()
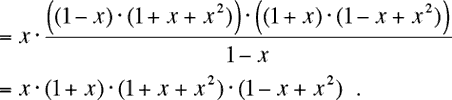
De donde
r·g = x2·(1+x)2·(1+x+x2)2·(1-x+x2)2 = r*·g*.
Por nuestro acuerdo anterior de que el número más pequeño en cada dado es un 1, cada uno de r* y g* debe tener x como un factor. Ya que la suma de los coeficientes en los factores (1+x), (1+x+x2), y (1 – x + x2) son respectivamente 2, 3, y 1, la única forma de obtener una suma de 6 es usar 1+x y 1+x+x2 como factores en ambos r* y g*. De donde la única opción que tenemos es donde poner los dos factores 1 – x + x2. Si uno va con r* y el otro con g*, regresamos a donde empezamos. La otra opción es ponerlos juntos – en digamos g*. De donde
r* = x·(1+x)·(1+x+x2) = x + 2x2 + 2x3 + x4 (=x + x2 + x2 + x3 + x3 + x4),
y
g* = x·(1+x)·(1+x+x2)·(1-x+x2)2 = x + x3 + x4 + x5 + x6 + x8.
Obtenemos la única solución básica al leer los exponentes de r* y g*. Como en la solución directa, vemos que la única alternativa para los dados comunes es el par con caras r* = (1, 2, 2, 3, 3, 4) y g* = (1, 3, 4, 5, 6, 8). Por cierto, note que los coeficientes en todos los polinomios que aparecen en estas factorizaciones y productos tienen una simetría obvia. Esta es precisamente la simetría que usamos para simplificar nuestra primera solución.