Las longitudes de los lados consecutivos de un cuadrángulo plano son 6,33,47 y 34. ¿Cuál es el ángulo entre las dos diagonales?
(Aunque estas longitudes parecen haber sido escogidas al azar, no lo fueron)
Este mes recibimos soluciones correctas de
Mehdi Abdeh-Kolahchi (Halifax) |
Xavier Hecquet (Francia) |
|
Theerasak Asawanonwiwat (Tailandia) |
Eric Hsiung (EU) |
|
Bernard Carpentier (Francia) |
Normand LaLiberté (Ontario) |
|
K.A. Chandrashekara (.com) |
Arne Loosveldt (.com) |
|
Pablo de la Viuda (España) |
Patrick LoPresti (EU) |
|
H.N. Gupta (Regina) |
Wolfgang Kais (Alemania) |
Respuesta:
El ángulo entre las dos diagonales es 90º.
Todos sabemos que si se fijan los lados de un triángulo, se fija su forma. Al contrario, la forma de nuestro cuadrilátero ABCD no es fijo aún cuando la longitud de sus lados se han fijado en 6, 33, 47, y 34: si usted construye un cuadrilátero con cuatro palillos con bisagras en los vértices, puede usted deformarlo — o "smoosh it around", en las palabras deLoPresti — como se puede hacer con el cuadrilátero en la Figura 1. (Puede usted mover el punto C sin cambiar las longitudes p, q, r, s.) Escogemos los lados p, q, r, s en la Figura 1
Figura 1
Para que se tenga p + s = q + r, haciendo obvio que el ángulo entre AC y BD no es constante — usted puede ver que se va de positivo a cero conforme A y C se mueven hacia la diagonal BD. Es por lo tanto muy sorprendente que cuando AC es perpendicular a BD en una posición dada, permanecerá perpendicular en todas las posiciones (como en la Figura 2, en la cual, otra vez, A puede
Figura 2
ser movida.) En efecto, en su solución Chandrashekara simplemente se refirió al teorema de Peaucellier:
La suma de los cuadrados de los lados opuestos de un cuadrilátero son iguales si y solamente si las diagonales son perpendiculares.
En nuestro cuadrilátero, p = 6, q = 33, r = 47, y s = 34, entonces
p2 + r2 = 62 + 472 = 2245 = 332 + 342 = q2 + s2.
Discutiremos la historia del teorema y su importancia al final. Primero presentamos tres demostraciones diferentes, cada una restringida a nuestro caso específico. Usted puede remplazar los cuatro números dados p, q, r, s para obtener la demostración general con cada versión diferente.
1. Demostración por coordenadas.
Modificaremos la solución de Hecquet al escoger el vértice B como el origen y remplazando D como el punto (k, 0) en el eje x. El punto A entonces será uno de los dos puntos donde el círculo centrado en B de radio 33 se intercepta con el círculo centrado en D de radio 6. Las coordenadas (x, y) de A por lo tanto deben satisfacer
x2 + y2 = 332 = 189 y (x - k)2 + y2 = 62 = 36.
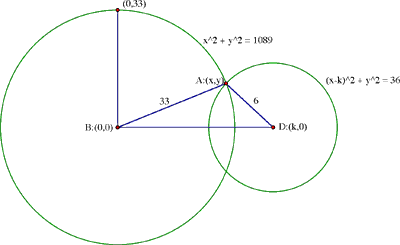
Figura 3
Substraiga la segunda de la primera para encontrar que 2kx – k2 = 1053, de tal manera que la x-coordenada de A debe satisfacer
Similarmente, las coordenadas (x, y) de C satisfacen
x2 + y2 = 472 = 2209 y (x - k)2 + y2 = 342 = 1156.
Substrayendo la segunda de la primera, vemos que la x-coordenada de C debe ser igual a la x–coordenada de A. Esto es, ambos A y C yacen en la línea vertical x = (1053 + k2)/2k; en otras palabras, AC es perpendicular a BD.
2. Demostración usando las ley de los cosenos (el método de Abdeh-Kolahchi, Asawanonwiwat, Carpentier, Chandrashekara, de la Viuda, LaLiberté, Loosveldt, y LoPresti). Presentaremos una combinación de las versiones similares de Abdeh-Kolahchi, de la Viuda, y LoPresti. Sean las diagonales AC y BD que se interceptan en P (indicadas en la Figura 2). Denote las distancias de P a A, B, C, y D por a, b, c, y d, respectivamente, y sea q <APB. Recuerde que cos q = –cos(180º – q). Por la ley de los cosenos aplicada en turno a los triángulos APB, BPC, CPD, y DPA,
332 = a2 + b2 – 2ab cos q, 472 = b2 + c2 + 2bc cos q, 342 = c2 + d2 – 2cd cos q, 62 = d2 + a2 + 2da cos q. |
 |
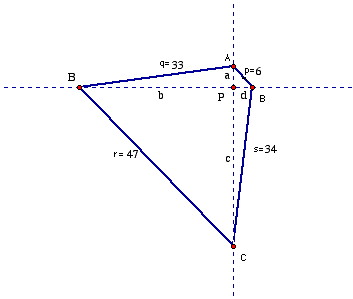Substrayendo la primera y terceras ecuaciones de la suma de la segunda y cuarta, encontramos que
472 + 62 –332 – 342 = 2(ab + bc + cd + da) cos q
Ya hemos visto que el lado de la izquierda es 2245 – 2245 = 0. Si podemos demostrar que 2(ab + bc + cd + da) > 0, se seguirá inmediatamente que cos q = 0, de tal manera que q = 90º, como se deseaba. Ya que ab + bc + cd + da = (a + c)(b + d) = AC·BD, y ya que todos los a, b, c, d representan distancias de P, fueran a + c cero, tendríamos (por definición) A = C = P; pero A y C no podrían yacer ambas en BD ya que 33 + 6 ≠ 47 + 34. Similarmente, b + d ≠ 0, así que su producto es también no cero, esto termina la demostración.
3. Demostración usando el Teorema de Pitágoras. (Este es el método de Gupta, Hsiung, y de la segunda demostración de Carpentier.)
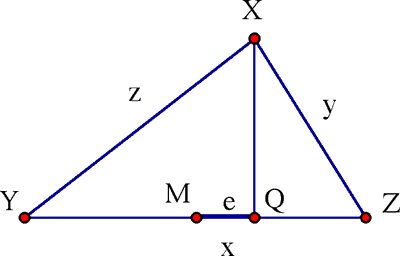
Figura 4
Lema. En cualquier triángulo XYZ cuyos lados satisfacen z ≥ y, la altitud de X intercepta los lados opuestos YZ en un punto Q cuyas distancias del punto medioes
Demostación. Pitágoras nos dice que XQ2 = YX2 – YQ2 = ZX2 – ZQ2, de tal manera que
Expandiendo y simplificando, obtenemos z2 – y2 = 2xe, así que e = ( z2 – y2)/2x como se afirmaba.
Aplicamos el lema a nuestros triángulos originales ABD y CBD. En la Figura 2 arriba tenemos DABD en la parte superior con z = 33, y = 6, y X = BD, así que
Abajo, tenemos DCBD con z = 47, y = 34, y x = BD, así que
Tiene el mismo valor. De donde las perpendiculares a BD de A y de C interceptan BD a la misma distancia del punto medio. Ya que puede haber solamente una línea perpendicular a BD en ése punto, esa línea debe ser la diagonal AC; concluimos que AC es perpendicular a BD.
Antecendente histórico.
Charles-Nicolas Peaucellier (1832-1913) era capitán en el cuerpo de ingenieros de la artillería Francesa en 1864 cuando inventó la célula Peaucellier ["... presentada en términos generales y en forma cuestionada en los Nouvelles Annales mathématiques, página 414; su exposición detallada apareció en la misma revista en 1873, página 71."]. Esta célula Peaucellier es una cadena que arrastra la inversa de cualquier locus, dando entonces por primera vez una solución exacta al problema mecánico de convertir un movimiento circular en un movimiento lineal: en Figura 5, como D traza un circulo pasando a través de B, D' se mueve a lo largo de una línea perpendicular al diámetro a través de B de ése circulo. El adminículo esta formado por dos varillas de longitud r y dos de longitudes s, con bisagras en las esquinad A y C de un cuadrángulo con la forma de un cometa ADCD', con varillas mas largas de longitud p y q conectando las esquinas opuestas A y C a un pivote fijo en B. Como
figura 5
consecuencia de este teorema, el producto BD·BD' será constante. La demostración de esta afirmación es similar al argumento que usamos en la demostración 3 como sigue (vea la Figura 6): p2 – b2 = a2 = s2 – d2, y así
p2 – s2 = b2 – d2 = (b – d)·(b + d) = BD·BD'.
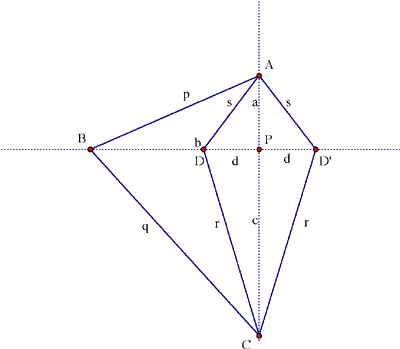
figura 6
Bajo la hipótesis que p2 – s2 = q2 – r2 (la cual hemos
visto es equivalente a AC perpendicular a BD cuando los lados más
largos p y q llegan del mismo vértice) el producto BD·BD'
es constante cuando las longitudes p, q, r, y s son fijas. Por definición
esto significa que D' será la inversa del punto D en un circulo
cuyo centro es B y radio es 
. Entonces,
con D como punto fijo se traza sobre las curves de la figura dada, un
lápiz se coloca en D' y se dibuja la figura; en particular, si
una séptima varilla y otro pivote se introducen para conservar
D en un circulo que pase a través de B, el locus de D' será una
línea recta. La historia completa se menciona en unos libros de
geometría que discuten inversión (tales como H.S.M. Coxeter, Introduction
to Geometry, Capítulo 6), o libros que tratan con la geometría
de los números complejos (bajo los nombres de fracciones lineales
o transformaciones de Möbius). Vea también las páginas
de web
http://mathworld.wolfram.com/Inversion.html y http://www.cut-the-knot.org/pythagoras/invert.shtml .
Hay muchas otras páginas de web que discuten la célula de Peaucellier; simplemente pídale a Google que las encuentre por usted. Encontramos el nombre y vida completos de Peaucellier en la página http://sunsite.utk.edu/math_archives/.http/hypermail/historia/feb99/0014.html. (No hemos confirmado esta información.) Tomamos esta información sobre el teorema de Peaucellier de Exercices de géométrie, 4th ed (1907), by F. G.-M, páginas 505, 506, y 513.