Doble-trueque
Este mes mostramos como la televisión puede ser usada con propósitos educativos. Suponga que usted tiene dos televisiones una al lado de la otra, la Televisión A y la Televisión B, están activadas por dos controles remotos distintos. Llamamos doble-trueque al acto de apretar simultáneamente los botones de los controles remotos que cambian los canales de las televisiones A y B a los canales inmediatos superiores o inferiores.
Por ejemplo, de (Canal 8, Canal 6) puede pasar a cualquiera de los canales (Canal 7,Canal 5), (Canal 7,Canal 7), (Canal 9,Canal 5) o (Canal 9,Canal 7).
Pare el problema de este mes tiene usted tres televisiones una al lado de la otra, cada una activada con su propio control remoto (distintos) y conectadas a diferentes compañías de cable:
Televisión A esta conectada a la compañía de cable Alfa que tiene 70 canales, del A1 al A70,
Televisión B esta conectada a la compañía de cable Beta la cual tiene 60 canales, del B1 al B60, y
Televisión C esta conectada a la compañía de cable Gama que tiene 94 canales, del C1 al C94.
Sin embargo, encuentra usted que hay pocas redes transmisoras diferentes, cada una de ellas es duplicada una y otra vez, aún mas las redes son exactamente las mismas en las tres compañías de cable; en particular, el canal A1 es el mismo que el canal B1 y el canal C1, y el canal A70 es el mismo que el canal B60 y C94. Eventualmente encuentra usted que es posible empezar de (A1,B1) y hacer doble-trueque hasta terminar con (A70,B60) en tal forma que el programa en la televisión A es siempre el mismo que el programa en la televisión B. Similarmente, es posible empezar en (B1,C1) y hacer doble-trueque hasta terminar con (B60,C94) en tal forma que el programa en la televisión B es siempre el mismo en la televisión C.
El problema de febrero. Bajo estas condiciones es posible hacer doble-trueque de (A1,C1) a (A70,C94) en tal forma que el programa en la televisión A es siempre el mismo que el programa en la televisión C.
Precaución. No trate de apretar el botón para pasar al canal inmediato inferior cuando la televisión esta en el canal 1; similarmente no trate de apretar el botón para pasar al canal inmediato superior cuando la televisión esta en el canal máximo. Esto pudiera hacer que la televisión correspondiente explote, y su seguro puede quedar anulado
Solución de MP48
Si, siempre es posible hacer doble-trueque de (A1, C1) a (A70, C94) de tal manera que el programa en la pantalla de la televisión A es siempre el mismo que el de la pantalla de la televisión C. Aún mas, es posible hacer doble-trueque de (A1,B1,C1) a (A70,B60,C94); una faena que vale bien la pena tratar para aquellos que son suficientemente diestros con el pie derecho.
Recibimos una solución parcial de Xavier Hecquet (Francia), donde indicó que el problema es más fácil de resolver cuando todos los canales en B son diferentes. En este caso, podemos ir de (A1,B1) a (A70,B60) al apretar siempre el botón del control remoto de A que cambia el canal al canal inmediato superior. En efecto, Si apretamos el botón del canal inmediato superior de A para ir de (Ai,Bj) a (Ai+1,Bj') y luego apretamos el botón del canal inmediato inferior para ir a (Ai,Bj''), entonces j'' = j (ya que todos los canales de B son diferentes), así que los dos últimos pasos se cancelan uno con el otro. Resolveremos el caso donde todos los canales en B son diferentes.
Solución 1. Todos los canales de B son diferentes.
Formaremos una gráfica G cuyos vértices son todas la parejas (Ai,Ck) que corresponden a un Bj en común, y donde las dos parejas (Ai,Ck) y (Ai',Ck') están conectadas si podemos hacer doble-trueque de una pareja a la otra.
Programas |
|||
Canal |
Compañía |
Compañía |
Compañía |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
3 |
1 |
3 |
3 |
4 |
2 |
|
2 |
5 |
3 |
|
3 |
6 |
2 |
|
2 |
7 |
1 |
|
3 |
8 |
2 |
|
2 |
9 |
3 |
|
3 |
Por ejemplo la tabla de arriba corresponde a un ejemplo mas pequeño que tiene cuatro canales diferentes, y A, C tienen nueve canales cada uno. La gráfica G que consideramos es la siguiente.
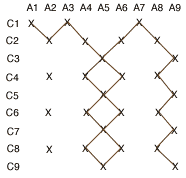
Entre otras cosas, la gráfica contiene algunos vértices aislados como (A2,C6), y el trayecto largo (A1,C1), (A2,C2), (A3,C1), (A4,C2),(A5,C3), (A6,C2), (A7,C1), (A8,C2), (A9,C3), (A8,C4), (A9,C5), (A8,C6), (A9,C7), (A8,C8), (A9,C9). Demostraremos que tal trayecto de (A1,C1) a (Aúltimo,Cúltimo) necesariamente existe, usando la siguiente propiedad local de la gráfica.
Lema 1: Si A tiene m canales y C tienen n canales, entonces (A1,C1) y (Am,Cn)tienen exactamente un vecino cada uno, y todos los otros vértices de G tienen un número par de vecinos.
Demostración. Asuma que la pareja (Ai,Ck) corresponde a Bj, donde 1 < i < m y 1 < k < n.
Ya que podemos hacer doble-trueque de (A1,B1) a (Am,Bt) (donde t es el número de canales de B), los canales Ai-1 y Ai+1 corresponden cada uno a uno de Bj-1, Bj+1. Similarmente, ya que podemos hacer doble-trueque de (B1,C1) a (Bt,Cn), los canales Ck-1 y Ck+1 corresponden cada uno a uno de Bj-1, Bj+1. Por ejemplo, Ai-1 y Ck-1 podrían corresponder a Bj-1, y Ai+1, Ck+1 podría corresponder a Bj+1, y entonces (Ai,Ck) tienen los dos vecinos (Ai+1,Ck+1) y (Ai-1,Ck-1). Hay dieciséis casos similares en total los cuales mostramos en la tabla de abajo.
vecinos de (Ai,Ck) |
Ck-1 = Bj-1 Ck+1 = Bj-1 |
Ck-1 = Bj-1 Ck+1 = Bj+1 |
Ck-1 = Bj+1 Ck+1 = Bj-1 |
Ck-1 = Bj+1 Ck+1 = Bj+1 |
Ai-1 = Bj-1 Ai+1 = Bj-1 |
(Ai-1,Ck-1) (Ai-1,Ck+1) (Ai+1,Ck-1) (Ai+1,Ck+1) |
(Ai-1,Ck-1) (Ai+1,Ck-1) |
(Ai-1,Ck+1) (Ai+1,Ck+1) |
|
Ai-1 = Bj-1 Ai+1 = Bj+1 |
(Ai-1,Ck-1) (Ai-1,Ck+1) |
(Ai-1,Ck-1) (Ai+1,Ck+1) |
(Ai-1,Ck+1) (Ai+1,Ck-1) |
(Ai+1,Ck-1) (Ai+1,Ck+1) |
Ai-1 = Bj+1 Ai+1 = Bj-1 |
(Ai+1,Ck-1) (Ai+1,Ck+1) |
(Ai-1,Ck+1) (Ai+1,Ck-1) |
(Ai-1,Ck-1) (Ai+1,Ck+1) |
(Ai-1,Ck-1) (Ai-1,Ck+1) |
Ai-1 = Bj+1 Ai+1 = Bj+1 |
|
(Ai-1,Ck+1) (Ai+1,Ck+1) |
(Ai-1,Ck-1) (Ai+1,Ck-1) |
(Ai-1,Ck-1) (Ai-1,Ck+1) (Ai+1,Ck-1) (Ai+1,Ck+1) |
Entonces en todos los casos, vemos que (Ai,Ck) tiene 0, 2 o 4 vecinos.
En las fronteras ocurren excepciones, esto es, cuando i = 1 o m, o k = 1 o n. Cuando i = 1 y 1 < k < n, tenemos A1 = B1 = Ck de dobde A2 = B2 = Ck-1 = Ck+1, así que (A1,Ck) tiene los dos vecinos (A2,Ck-1) y (A2,Ck+1). Similarmente, todas las parejas de tipo (Am,Ck), 1 < k < n, (Ai,C1) o (Ai,Cn), 1 < i < m tienen exactamente dos vecinos. Las dos parejas (A1,C1) y (Am,Cn) tienen cada una un vecino, respectivamente (A2,C2) y (Am-1,Cn-1), y ninguna de las parejas (A1,Cn) y (An,C1) pertenecen a la gráfica ya que A1 = B1 la cual es diferente de Bt = Cn, y An = Bt la cual es diferente de C1 = B1. Esto demuestra el lema.
El número de vecinos de un vértice de una gráfica es llamado el “grado” del vértice. Lema 1 afirma que cada vértice en nuestra gráfica tiene grado par, excepto (A1,C1) y (Am,Cn), el cual tienen grado 1. Uno de los resultados básicos en la teoría de gráficas es el siguiente.
Lema 2. En cualquier gráfica, el número de vértices de grado non es par.
Demostración corta: Si sumamos todos los grados de los vértices en una gráfica obtenemos dos veces el número de aristas, porque contamos cada vértice dos veces.
Entonces podemos dividir esta suma por 2 y obtener el número de aristas, lo cual es un número entero. Por lo tanto el número de grados non es par. Esto es todo. Una observación simple es la llave para la solución de Euler al problema del puente Königsberg.
Note que es consistente con lo que sabemos de G, lo cual es exactamente dos vecinos de grado non, esto es (A1,C1) y (Am,Cn). ¿Hay algo mas que decir? Si! Lo que necesitamos hacer es aplicar el Lema 2 a un gráfica mas pequeña H que consiste de los vértices de G que son alcanzables de (A1,C1) por una secuencia de trueques dobles. Esto es, (A1,C1) esta en H, y siempre que un vértice (Ai,Ck) de G esta en H, entonces todos sus vecinos también están en H. Ya que H contiene el vértice (A1,C1) de grado 1, debe contener un segundo vértice de grado non. Sin embargo el único candidato es (Am,Cn), lo que significa que (Am,Cn) debe también pertenecer a H. Por lo tanto es posible moverse de (A1,C1) a (Am,Cn) por una secuencia de trueques dobles.
Desafortunadamente este bello argumento no funciona para cuando los canales de B se repiten. Por ejemplo, en nuestro ejemplo de arriba, si remplazamos todos los 3es por 1s, entonces necesitamos añadir muchos vértices de G, incluyendo (A1,C9) el cual será de grado 1. Veremos abajo como adaptar la demostración al caso general.
Solución 2. El caso general.
Sean las televisiones A, B y C con canales m, t y n respectivamente, sean estos A1 a Am, B1 a Bt y C1 a Cn. Es posible hacer doble trueque de(A1,B1) a (Am,Bt) de tal manera que un programa en A es siempre el mismo en B, y de (B1,C1) a (Bt,Cn) en tal forma que el programa en B es siempre el mismo al programa en C entonces es posible hacer doble trueque de (A1,C1) a (Am,Cn) en tal forma que el programa en A es siempre el mismo al programa en C.
Demostración: Por simplicidad llamaremos a un doble trueque “coherente” cuando brinca del canal idéntico a canal idéntico. Sea P un camino que corresponde a la secuencia mas corta de doble trueques coherentes de (A1,B1) a (Am,Bt). Esto es P = { (A1,B1), (A2,B2), (Ai3,Bi3),= (Ai4,Bi4), ..., (Am-1,Bt-1), (Am,Bt)}. El mismo canal Ai puede ser la primera coordenada de muchas parejas en P, y el mismo canal Bj puede ser la segunda coordenada de muchas parejas en P. Sin embargo una pareja (Ai,Bj) no puede ocurrir dos veces en P, de otra manera habría un atajo a P. Similarmente, sea Q = {(B1,C1), (B2,C2), (Bj3,Cj3), ..., (Bt-1,Cn-1),= (Bt,Cn)} un camino que corresponde a la secuencia mas corta de doble trueques coherentes de doble trueques de (B1,C1) a (Bt,Cn). Formamos la gráfica G cuyos vértices son los triples (Ai,Bj,Ck) tal que (Ai,Bj) esta en P y (Bj,Ck) esta en Q, donde (Ai,Bj,Ck) esta unido a (Ai',Bj',Ck') cuando (Ai,Bj) es un vecino de (Ai',Bj') en P y (Bj,Ck) es un vecino de (Bj',Ck') en Q.
Demostraremos otra vez que (A1,B1,C1) y (Am,Bt,Cn) son los vértices de grado non en G, y como en la solución 1, esto significa que existe una secuencia coherente de trueques triples que empieza en (A1,B1,C1) y termina en (Am,Bt,Cn).
Lema 3: Todos los vértices en G tienen un grado par, excepto (A1,B1,C1) y (Am,Bt,Cn) el cual tienen grado 1.
Demostración del lema 3: Sea (Ai,Bj,Ck) un vértice de G. Usualmente, (Ai,Bj) tendrá dos vecinos (Ai',Bj'), (Ai'',Bj'') en P, y (Bj,Ck) tendrá dos vecinos (Bj''',Ck'), (Bj'''',Ck'') en Q. Esto significa que cada uno de las i', i'' es i-1 o i+1, cada una de las j', j'', j''', j'''' es j-1 o j+1, y cada una de las k', k'' es k-1 o k+1. Los vecinos posibles de (Ai,Bj,Ck) son las cuatro triples (Ai',Bj',Ck'), (Ai',Bj',Ck''), (Ai'',Bj'',Ck') y (Ai'',Bj'',Ck''). (Ai',Bj',Ck') es un vecino de (Ai,Bj,Ck) si y solo si j' = j''', (Ai',Bj',Ck'') es un vecino de (Ai,Bj,Ck) si y solo si j' = j'''', (Ai'',Bj'',Ck') es un vecino de (Ai,Bj,Ck) si y solo si j'' = j''' y (Ai'',Bj'',Ck'') es un vecino de (Ai,Bj,Ck) si y solo si j'' = j''''. Ya que todas las j', j'', j''' y j'''' son j-1 o j+1, el número de igualdades entre j', j'' por un lado y j''', j'''' por el otro es par, por lo tanto el grado de (Ai,Bj,Ck) es par. Se ve fácilmente que los casos fronterizos de tipo(A1,B1,Ck), (Am,Bt,Ck), (Ai, B1,C1) y (Ai,Bt,Cn) son de grado 2, excepto para (A1,B1,C1) y (Am,Bt,Cn) los cuales son de grado 1. Esto concluye la demostración del lema y nuestra solución.