
El círculo unitario se divide en doce partes iguales, y los doce puntos que lo
dividen se unen al centro del círculo, produciendo doce rayos. Empezando por uno
de los puntos que lo divide se dibuja un segmento de linea perpendicular al
próximo rayo en la direccion de la manecillas del reloj; a partir del pie de esta
perpendicular otra perpendicular se dibuja al próximo rayo, y asi sucesivamente.
¿Cual es le limite de la suma de estos segmentos?
Solución de MP43
| Alex Akulov (Regina) | Wolfgang Kais (Alemania) |
| Said Amghibech (Quebec) | Normand LaLiberté (Ontario) |
| Endre Balogh (Hungria) | Patrick LoPresti (USA) |
| Ricardo Barroso Campos (España ) | Marian Marinescu (Francia) |
| Pierre Bornsztein (Francia) | Juan Mir Pieras (España ) |
| Bernard Carpentier | Leigh Norris (E.U.) |
| Bruno Demarest (Francia(?)) | Fernando Szechtman (Regina) |
| Xavier Hecquet (Francia) | AWD ‘Silversprite’ |
| Pablo de la Viuda (España) |
Bienvenidos nuestros viejos amigos, y bienvenidos todos los recién llegados. Gracias por sus interesantes soluciones.
Todos sumaron los términos de una seria para determinar que la longitud del camino es
![]()
Después de presentar la solución común, veremos dos soluciones geométricas de Xavier Hecquet, y varias generalizaciones de Kais, Mir, and Szechtmen.
La solución usando series.
Sea O el centro, sea P0 el punto inicial de un círculo unitario, y sea P1, P2, ..., los pies de las perpendiculares sucesivas. Los triángulos que resultan OPnPn+1 son triángulos rectángulos con ángulos de 30º en O y 60º en Pn:
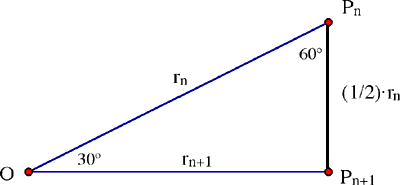
La hipotenusa rn+1 = OPn+1 del siguiente triángulo es el producto de cos (30º) y la hipotenusa rn de éste triángulo. Ya que cos (30º) = √3/2, tenemos
![]()
El camino poligonar cuya longitud estamos calculando esta compuesta de los lados PnPn+1 de triángulos sucesivos; estos tienen longitud rnsin(30º) = rn/2. En consecuencia, en el siguiente triángulo la contribución es
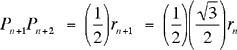
La suma de los primeros n+1 segmentos es por lo tanto
P0P1 + P1P2 + P2P3 + ... + PnPn+1 = 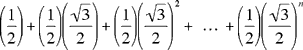
Lo cual reconocemos como una progresión geométrica con radio √3/2; y es
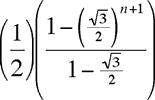
Ya que √3/2 < 1, (√3/2)n+1 se aproxima a 0 cuando n tiende a infinito, se sigue que la suma del limite debe ser
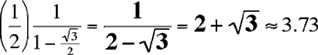
como se afirmaba.
Mirando el diagrama apropiado y usando algo de trigonometría básica, usted puede determinar la longitud del camino sin la fórmula de la suma infinita. De hecho, Hecquet nos envió dos diagramas que resuelven nuestro problema a primera vista.
Diagrama 1.
Desenredemos el camino deslizando cada triángulo OPnPn+1 a la posición OnP´nP´n+1 de tal manera que su lado recto P´nP´n+1 queda a lo largo de la extensión del lado P0P1. Estos son los triángulos azules rectos de 30-60 en la figura. (Quitemos las primas para simplificar la notación.) Ya que
el lado inferior (OnPn+1) de cada triángulo es igual a la hipotenusa (On+1Pn+1) del próximo, cada triángulo blanco OnPn+1On+1 es isósceles; todos son similares con un ángulo de 30º en Pn+1 y ángulos de 75º en On y On+1. Esto obliga a los O’s a estar a lo largo de una línea. En el limite, la línea de O’s y la línea of P’s se encuentra en el punto indicado P∞. La longitud del lado recto, o sea P0P∞, es la longitud del nuestro camino del polígono el cual ha sido enderezado. Completado la figura con una línea horizontal O´P0 de longitud 1 en la parte de arriba, obtenemos un triángulo recto con ángulo de 75º en O´ y 15º en P∞ (y ángulo recto en P0). La Longitud deseada es por lo tanto
P0P![]() =
1/cot(15º).
=
1/cot(15º).
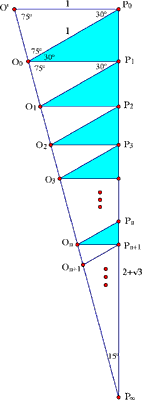
Para ver que esta es la misma respuesta obtenida en la solución de la serie, use la fórmula de ángulo medio:
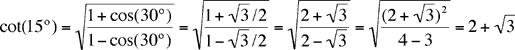
como se esperaba.
Diagrama 2.
Otra vez alineamos los triángulos de la secuencia, pero esta vez volteamos cada segundo triángulo, intercambiando O con P2k+1. Por ejemplo, volteamos el segundo triángulo P1OP2 de tal manera que O cambia de lugar con P1, y el lado P1P2 queda en el lado izquierdo
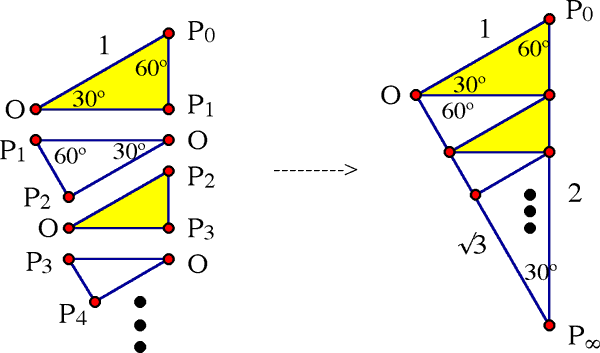
de la figura. Usted debe confirmar que la mitad de los segmentos
a lo largo del camino (cuya longitud vamos a determinar), o sea
P0P1, P2P3, …, P2kP2k+1, …, están alineados
a lo largo del lado derecho, mientras que los otros, P1P2, P3P4, …,
P2k+1P2k+2, …, están alineados a lo largo de la izquierda. (Puede
verse que los ángulos aseguran que estos segmentos están
a lo largo de líneas rectas.) Resultando que la figura
P0OP![]() es un triángulo recto 30-60 cuyo lado superior
tiene longitud1. El lado izquierdo OP
es un triángulo recto 30-60 cuyo lado superior
tiene longitud1. El lado izquierdo OP![]() por lo tanto tiene
longitud cot(30º) = √3, y su hipotenusa P0P
por lo tanto tiene
longitud cot(30º) = √3, y su hipotenusa P0P![]() tiene
longitud csc(30º) = 2. La longitud de nuestro camino
es la suma de estos dos números, 2 + √3.
tiene
longitud csc(30º) = 2. La longitud de nuestro camino
es la suma de estos dos números, 2 + √3.
Generalizaciones.
Todos
nuestro argumentos son fáciles de modificar si en lugar
de empezar con el círculo unitario dividido en doce partes
iguales, lo dividimos en n partes iguales. Mas generalmente, podríamos
poner los ángulos iguales PnOPn+1 = φ. La
longitud del camino es entonces 
Podemos también remplazar nuestras perpendiculares por segmentos hacia la siguiente línea en un ángulo arbitrario a < 90º. Mas precisamente,
Los puntos Q0, Q1, Q2, … están equitativamente distribuidos en dirección positiva sobre el círculo unitario y unidos al centro O. Definimos un camino poligonal P0P1P2… como sigue: Sea P0 = Q0, y defina P1 como el punto OQ1 para el cual el ángulo P0P1Q1 = α. Continúe de esta forma de la manera que Pn+1 es el punto para el cualel el ángulo PnPn+1Qn+1 = α. Encuentre la longitud limite del camino poligonal para cuando n tiende a infinito. .
Las pruebas con figuras dan una solución que
es ¡ingeniosamente
simple y sorprendente! En cada una de las figuras de arriba
simplemente remplazamos el ángulo de 30º (en
los puntos correspondientes a O) por φ, y los ángulos
de 60º (en los puntos correspondientes a Pn) por
α – φ,
como en las figuras de abajo. En el diagrama de la izquierda,
el triángulo grande PoO´P![]() tiene ángulos
a en P0 y 90º – φ/2 en O´; entonces,
el ángulo
en P
tiene ángulos
a en P0 y 90º – φ/2 en O´; entonces,
el ángulo
en P![]() debe
ser 180º – α – 90º + φ/2 = 90º – (α – φ/2). Como
queremos la longitud de P0P
debe
ser 180º – α – 90º + φ/2 = 90º – (α – φ/2). Como
queremos la longitud de P0P![]() , aplicamos la ley de los senos a éste
triángulo
(la cual dice que el cociente de un lado dividido por el seno del ángulo
opuesto es el mismo para todos los otros tres lados.) Esto
es,
, aplicamos la ley de los senos a éste
triángulo
(la cual dice que el cociente de un lado dividido por el seno del ángulo
opuesto es el mismo para todos los otros tres lados.) Esto
es,
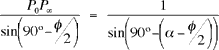 ,or
,or 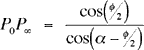
Se necesitan algunas identidades trigonométricas para ver que esto coincide con la respuesta esperada cuando α = 90º como en el problema original:
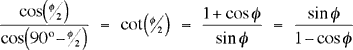

En la Segunda figura, otra vez P0OP![]() es
un triángulo,
ahora con ángulos a – φ en P0,a en O’, y (por
lo tanto) 180º – (2α – φ) en P
es
un triángulo,
ahora con ángulos a – φ en P0,a en O’, y (por
lo tanto) 180º – (2α – φ) en P![]() . Por
la ley de los senos — y usando sin(180º – (2α – φ)) = sin(2α – φ) — vemos que
. Por
la ley de los senos — y usando sin(180º – (2α – φ)) = sin(2α – φ) — vemos que
 and
and 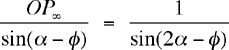
De donde, la longitud del camino es P0P![]() +
OP
+
OP![]() =
= 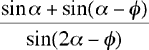
Mas vale que estas dos direcciones diferentes nos den la misma respuesta. Esto quiere decir, por supuesto, que
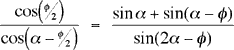
Esta es una identidad trigonométrica que muy probablemente no se le encuentra en los libros de texto.
Comentario. Note que si a f (el ángulo entre líneas de rayos sucesivos en O) se le permite disminuir a cero, el polígono espiral tiende hacia la espiral equiangular (o espiral logarítmica) cuya ecuación en coordenadas polares es r = e(cot α)θ. La curva intercepta cada línea de rayos (infinitamente) en un ángulo constante a. Puede encontrar mas información sobre
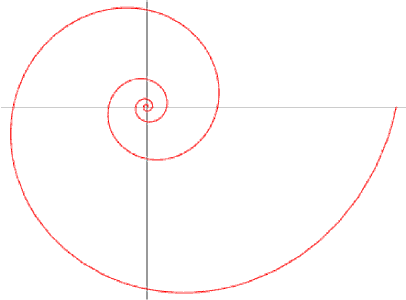
la curva en la página de web Mathworld
http://mathworld.wolfram.com/LogarithmicSpiral.html,
(de donde tomamos la figura) y en A Book of Curves de E.H. Lockwood (Cambridge University Press, 1971, Capítulo 9, páginas 98-109). Lockwood sugiere una forma de dibujar la curva: primero construya los puntos Pn de un polígono espiral usando un ángulo pequeño φ(como φ = 10º), entonces conecte a mano los puntos así encontrados en una curva. También él discute la “paradoja” que una curva sin fin podría tener una longitud finita, señalando que, “depende del significado preciso al cual nosotros le damos a la palabra fin. A pesar de que no hay un punto en sí en la curva el cual puede describirse como el punto final, hay sin embargo un punto, llamado el polo O, al cual la curva se aproxima y más allá al cual no llega.” Continúa produciendo una figura que es la versión infinita de la primera figura de Hecquet.
Otra generalización.
Szechtman toma en consideración lo que pasaría si se divide el círculo en n partes iguales y se suman solamente los primeros n segmentos a lo largo del camino que resulta. Para esto necesitamos medir nuestros ángulos en radianes, así que cambiamos la notación para el ángulo entre líneas de rayos sucesivos de f a x = 2π/n. Procedemos como en el problema original, dibujando perpendiculares de cada punto a la próxima línea. Como antes, encontramos que la suma de los primeros n segmentos es
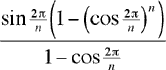
Ahora hacemos tender n a infinito. El ángulo x = 2π/n tiende a cero y un solo giro de la espiral se aproxima a un círculo unitario. Esto significa que si definimos

entonces el limite de f(x) cuando x tiende a 0 por la derecha mas vale que sea 2π. Para aquellos lectores que saben la regla de l’Hôpital o series de Taylor, es un buen ejercicio demostrar que 2π es en efecto el limite correcto.