Solución del problema de abril, 2007

El problema:
	Decimos que dos puntos sobre una esfera son ortogonales si las rectas que unen dichos puntos al centro de la esfera son perpendiculares. Por ejemplo, el polo norte es ortogonal a cualquier punto del ecuador, y no es ortogonal a ningún otro punto. Cuál es el mínimo número de colores necesarios para colorear la esfera de manera que ningún par de puntos ortogonales tenga el mismo color?

Respuestas correctas:
	Recibimos respuestas correctas de  Gérard Billion (Francia), Dan Dima (Rumania), Philippe Fondanaiche (Francia), Xavier Hecquet (Francia), Matthew Lim (USA), John T. Robinson (USA), y K. Sengupta (India)

La solución:

Se necesitan al menos cuatro colores. Tres no son suficientes.

Lamentablemente no todas las respuestas fuero tan completas como deseábamos. Como hace notar Fondanaiche, hay algunas sutilezas en la solución. Nos menciona varias referencias, incluyendo

A.W. Hales y E.G. Straus. Projective colorings. Pac. J. Math. 99:31-43, 1982,

    y

C. D. Godsil y J. Zaks. Coloring the sphere. University of Waterloo research report CORR 88-12, 1988. 

Se pueden encontrar otras referencias en la página

 http://tph.tuwien.ac.at/~svozil/publ/blatter.htm.

Entre otras cosas, Godsil y Zaks prueban que los puntos de la esfera con coordenadas racionales pueden ser coloreados con tres colores de manera que puntos ortogonales tengan colores diferentes. Dado que los puntos de coordenadas racionales son densos en la esfera, dicho  resultado muestra que no puede ser trivial mostrar que tres colores no son suficientes.

Parte 1: Tres colores no son suficientes.
            He aquí el método de Matthew Lim's para mostrar la insuficiencia de tres colores. Asumamos que podemos colorear la esfera unidad x² + y² + z² = 1 con tres colores de manera que puntos ortogonales tienen diferente color. Entonces cualquier círculo máximo (esto es, círculos cuyo plano contenga al origen) debe tener al menos dos colores (porque tiene pares de puntos octogonales) pero no puede tener los tres colores porque los dos polos (los puntos ortogonales a todos los puntos del círculo máximo) deben tener el tercer color. Los puntos

I = (1, 0, 0),   J = (0, 1, 0),  y K = (0, 0, 1)

son mutuamente ortogonales, de manera que tienen que recibir colores distintos, digamos rojo, azul y verde. Consideremos

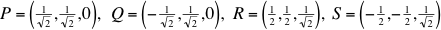
como en el diagrama. 

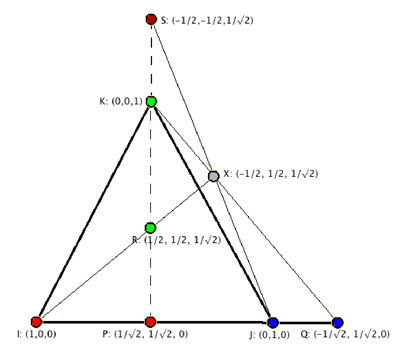
Como P y Q son ortogonales, deben tener colores diferentes; como están en el círculo máximo determinado por I y J, sus colores son rojo y azul. Supongamos por el momento que P es rojo y Q es azul. De manera similar, R y S son puntos ortogonales en el círculo máximo determinado por P y K; asumamos que R es verde y S es rojo. Sea X el punto con coordenadas (-1/2, 1/2, 1/√2): X está en el círculo máximo

IR determinado por el plano z = √2 y, luego su color es rojo o verde;
JS determinado por el plano  z = -√2 x , luego su color es rojo o azul;
KQ determinado por el plano y = –x, luego su color debe ser azul o verde.

Como X no puede satisfacer las tres condiciones al mismo tiempo, no es posible la coloración intentada. 
         ¿Qué pasaría si cambiáramos los colores de P y Q, o de R y S?. Siempre se pueden renombrar los puntos de manera que el argumento anterior se aplique con cambios menores: podemos remplazar I por su antípoda
I' = (–1, 0, 0) (que será rojo porque en un coloreado con tres colores, puntos antípodas siempre tendrán el mismo color); en este caso Q será un punto rojo en el arco que une el rojo I' y el azul J, y podemos poner R y S en el círculo máximo QK, revirtiendo los roles de P y Q. Similarmente, si R hubiera sido rojo y no verde, remplazamos R y K con los puntos antípodas de S y K. En todos los casos llegamos a un punto X que no puede ser coloreado apropiadamente, y concluimos que tres colores no son suficientes.

Part 2: Cuatro colores son suficientes.
Utilizaremos la regla de Billion para colorear la parte superior de la esfera, y completamos el trabajo usando la regla de que puntos antípodas reciben el mismo color. La primera figura muestra los triángulos esféricos abiertos sobre cada cuadrante en el plano xy que reciben los colores amarillo (sobre x, y > 0), rojo (sobre x < 0, y > 0), azul (sobre x, y < 0), y verde (sobre x > 0, y < 0). La segunda figura muestra el polo norte (azul), cuatro puntos que definen cuadrantes en el ecuador (dos amarillos, dos rojos), y los ocho arcos de círculo máximo que unen estos puntos. Debe chequearse que para cada punto en cada una de las figuras, el círculo máximo ortogonal a él está pintado con colores distintos.

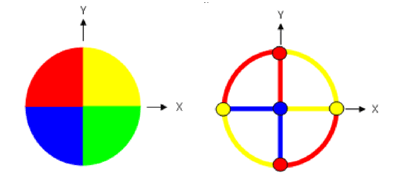
Vistas de la esfera desde arriba del polo norte.