Solución del problema de Noviembre, 2011

El problema:
	¿Existe una familia de circunferencias en el plano tales que todo punto del plano yace en exactamente dos de ellas? ¿Existe una familia de circunferencias en el plano tales que todo punto del plano yace en exactamente cien de ellas?

Respuestas correctas:

Sí, en ambos casos. Este problema fue propuesto en el "Tournoi des villes" in France in 1988, requiriendo 1988 círculos alrededor de cada punto del plano. Apareció más tarde en el libro Hypermath: 120 exercices de haut vol por Pierre Bornsztein (Vuibert, Paris, 2001). Agradecemos a Jean Doyen por mostrarnos el problema. Recibimos soluciones correctas de Bernard Collignon (Francia), Philippe Fondanaiche (Francia), Jan Fricke (Alemania), Benoît Humbert (Francia), Ile Ilijevski (Macedonia), y Patrick J. LoPresti (USA).

La solución:

Todas las soluciones fueron variaciones sobre la misma idea: usar tiras de círculos congruentes. Lo deja a uno pensando si hay básicamente una única aproximación al problema. La familia que utilizamos en (a)

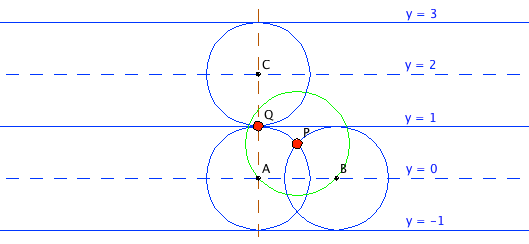
consiste de círculos de radio 1 en tiras horizontales: cada círculo tiene radio 1, y sus centros son los puntos $(x,y)$ con $x$ recorriendo todos los números reales, $y$ recorriendo los enteros pares. Los bordes de las tiras horizontales son las rectas $y=2n+1$. Mostramos dos típicas tiras de ancho 2 en la figura. Consideremos la tira con centro $y=0$: cualquier punto $P$ del interior de la tira está a distancia menor que 1 de $y=0$, mientras que está a distancia 1 de exactamente dos puntos en la línea ($PA=PB=1$ en la figura). Esos puntos son los centros de un par de círculos de la familia que pasan por $P$. Puntos $Q$ en el borde de la tira pertenecen a dos círculos tangentes, pertenecientes a cada una de las dos tiras que comparten la línea donde está $Q$. Como todo punto es o interior a una tira o está en un borde de una tira, todo punto del plano está en exactamente dos círculos de la familia, como se pedía.

En el caso de la pregunta (b) podemos tomar 50 copias de la familia utilizada en el primer caso; por supuesto, debemos asegurarnos de que los círculos de cada una de las 50 subfamilias son distintos de los de las otras 49. Mostraremos dos maneras de conseguirlo. Una forma es trasladando las líneas horizontales: es decir, centramos las tiras en $y = 2n + \frac{j}{50}, \; 0 \le j \le 49$. Así, los centros de los círculos de la familia $j$ estarán en la línea $y=2n + \frac{j}{50}$ y serán distintos de los de cualquier otra familia $k$ (que estarán en la línea $y=2n + \frac{k}{50}$) cuando $j \ne k$. Cada punto del plano estará en dos círculos de cada familia. La forma alternativa es obtener la familia $j$ dilatando los círculos de la solución (a) por un factor $j$, obteniendo círculos de diferentes radios en las diferentes familias.

Comentarios. Todos notaron que el argumento de la parte (b) se extiende de una manera natural para producir una familia de círculos que cubren los puntos del plano exactamente $N$ para cualquier entero par positivo. Humbert y LoPresti notó que no existe una familia de círculos tal que cada punto del plano yace en exactamente un círculo de la familia. Esto se debe a que si existiera tal familia, podríamos definir una sucesión $C_1, C_2, C_3, \cdots$ de sus círculos, donde $C_1$ es un miembro cualquiera de la familia y $C_i, i>1,$ es el único miembro de la familia que contiene el centro de $C_{i-1}$. Cada círculo $C_i$ está contenido en el interior de todos los círculos previos (porque contiene el centro de $C_{i-1}$ y no puede tener otro punto en común con ese círculo). Se deduce que para todo $i$ el radio de $C_i$ es menor que la mitad del radio de $C_{i-1}$, de manera que la sucesión de círculos converge a un punto. Pero este punto no puede pertenecer a ningún círculo de la familia porque tal círculo debería ser interior a todos los círculos $C_i$. No sabemos la respuesta al caso en que se requiere que cada punto pertenezca a un número impar (distinto de 1) de círculos.