Solución al problema de mayo, 2001

Todas las soluciones presentadas hicieron uso de los mismos dos pasos, pero cada una su propio enfoque. Para presentar los diferentes métodos, nuestra solución ha hecho uso trabajos presentados por:

Jeff Eggen (Manitoba, Canadá)
Normand Laliberté (Ontario, Canadá)
Leti Gimeno (Spain)
Juan Mir Pieras (España)
Alexander Potapenko (Russia)

1er. Paso - Determinar la altura de A hasta BC

Método (a)

Es posible evitar la necesidad de computación al reconocer que el triángulo 13-14-15 es un viejo conocido: la altura desde A parte al triángulo ABC en dos triángulos rectos, con lados 5-12-13 y 9-12-15; estos comparten el lado con largo de 12, que debe entonces de ser la altura del triángulo ABC. (Alternativamente, Gimeno nos recuerda que usando la ley del coseno obtenemos
,
del cual la altura es 12.)
Método (b) Usar el área (Mir y Potapenko) Para aplicar la fórmula de Heron para el área, computamos el semi-perímetro a ser s = (13 + 14 + 15)/2 = 21. Por lo tanto

.

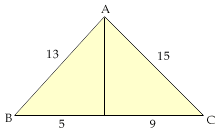
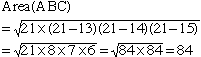Como la base BC =14, la altura correspondiente debe de ser (Área)/7 = 12 Método (c) Usando el teorema de Pitágoras (Eggen y Laliberté) Si H es el pié de la altura desde A, entonces

;

BH = 5, para que AH = 12. Este método concuerda con las matemáticas usadas en el método (a).

2do. Paso - Determinar el lado de cuadrado haciendo uso de que triángulo ADG ~ triángulo ABC.

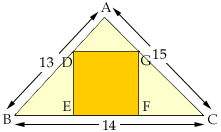
(Los triángulos son similares porque sus lados son paralelos.)


Tomemos x a ser el lado del cuadrado definido x=DE=EF=FG=DG.

Método (a) (Eggen, Potapenko y Laliberté)


y
.
Ya que las relaciones son iguales, tenemos  12-x/x = 12/14. Al solucionar para x, descubrimos que el largo del lado a determinar es x = 84/13. En realidad, Eggen y Laliberté usan trigonometría, que termina produciendo una computación similar. Método (b) Usar el área de las subfiguras (Gimeno) 84
= Area(ADG) + [Area(BED) + Area(GFC)] + Area(DEFG)
= (1/2)x(12 - x) + (1/2)x(14 - x) + x2
= 13x

El largo del lado del cuadrado es entonces de x = 84/13. Método (c) Mir

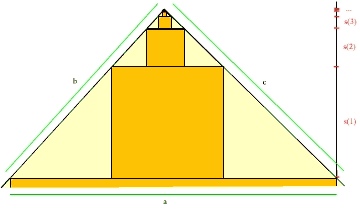
Considera una secuencia infinita de triángulos similares con los correspondientes cuadrados definidos dentro de cada uno. El triángulo original ABC y su cuadrado DEFG es contraído por un factor de k a un triángulo similar ADG con su cuadrado, y así sucesivamente. Si el largo de un lado del primer cuadrado es de x, entonces el cuadrado ADG tiene como largura de sus lados kx, y este cuadrado determina el próximo triángulo con su cuadrado con lados de k2x de largo, etcétera. Ya que los cuadrados ocupan la altura entera, tenemos:

   altura
= x + kx + k2x + ...
= x(1 + k + k2 + ...)
= x/1 - k
Para encontrar k, observamos que el lado del primer cuadrado es obtenido al contraer la base del triángulo original. Por lo tanto x=14k, y así k=x/14. El problema se reduce entonces a determinar


para x. Nuevamente computamos que x = 84/13.