Las manecillas de mi reloj se mueven de modo continuo. En el preciso instante en que el segundero pasa por una de las doce subdivisiones de la esfera, sé que en menos de medio segundo el minutero va a pasar justamente sobre el horario (la manecilla que indica la hora). A qué hora ocurre ésto, si es antes del mediodía?
Recibimos soluciones correctas de
Vincent Bardoux (Francia) |
Aleksandar Ilic (Serbia and Montenegro) |
|
Bernard Carpentier (Francia) |
Wolfgang Kais (Alemania) |
|
Philippe Fondanaiche (Francia) |
Matthew Lim (internet) |
|
Xavier Hecquet (Francia) |
Juan Mir Pieras (España) |
|
| Wilfrid Pillard (Francia) |
Solución.
La manecilla de la hora y el minutero se mueven a velocidad constante, de manera que hay un intervalo fijo entre los momentos en que apuntan en la misma dirección. El minutero pasa sobre la manecilla de la hora exactamente a medianoche, y coinciden 11 veces durante las siguientes doce horas. Esto significa que coinciden cada 12/11 horas; en otras palabras, el intervalo fijo entre un cruce y el siguiente es
1 hora, 5 minutos, 27 y 3/11 segundos.
(Como comprobación rápida, notar que cuando el minutero da 1 y 1/11 vueltas, la manecilla de la hora se mueve 1/11 de vuelta). Las dos manecillas coinciden entonces a las 1:05:(27+ 3/11), y de nuevo exactamente una hora, cinco minutos y 27+ 3/11 segundos más tarde a las 2:10:(54+ 6/11 ), y así siguiendo. Arribamos entonces a la lista de horarios en que el minutero cruza por encima de la manecilla de la hora:
Cruce |
hora |
minuto |
segundo |
1 |
1 |
5 |
27 + 3/11 |
2 |
2 |
10 |
54 + 6/11 |
3 |
3 |
16 |
21 + 9/11 |
4 |
4 |
21 |
49 + 1/11 |
5 |
5 |
27 |
16 + 4/11 |
6 |
6 |
32 |
43 + 7/11 |
7 |
7 |
38 |
10 + 10/11 |
8 |
8 |
43 |
38 + 2/11 |
9 |
9 |
49 |
5 + 5/11 |
10 |
10 |
54 |
32 + 8/11 |
11 |
12 |
0 |
0 |
El segundero ha pasado sobre una de las 12 subdivisiones cuando el número total de segundos es divisible por 5 a las 7:38:10 (coincidencia de la manecillas de la hora y el minutero ocurre 10/11 segundos después) y a las 9:49:05 (la coincidencia ocurre 5/11 segundos después). Como 5/11 es menos de un segundo, el cruce que buscamos ocurre menos de medio segundo antes de las 9:49:05 cada mañana.
Todas las soluciones presentaron una variación del argumento anterior. Además, Kais dio un segundo argumento que evita hacer una lista de posibilidades. Notar que la enésima coincidencia de las manecillas ocurre 12/11 
3600 n segundos después de la medianoche, y que
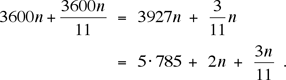
Estamos interesados en aquellos valores de n para los cuales
2n + (3n/11) es menos que ½ mayor que un entero múltiplo de 5:
(2 + 3/11) n < 5k + 1/2 .
Equivalentemente, 25n < 55k + 11/2, o
5n < 11k + 11/10.
En nuestro problema, n no puede ser 0; como 5n y 11k son ambos enteros, deben diferir exactamente por 1, y buscamos un valor de n entre 1 y 11 con 5n 
1 (mod 11). La inversa multiplicativa de 5 (mod 11) es –2 11 – 2 = 9 (mod 11). Como 5 y 11 son coprimos, sabemos que n 9 (mod 11) es la única solución. Nuevamente vemos que la única solución es n = 9a hora después de la medianoche.