Solución del problema de diciembre, 2006

El problema:

Para la temporada de fiestas ofrecemos un truco matemático para asombrar a amigos y parientes. No se requiere entrenamiento especial, solamente una mesa y 45 monedas. Ponga las 45 monedas en la mesa y pida a un voluntario que le vende los ojos a usted (este paso es opcional) y que después ordene las monedas en tantas pilas como quiera. Él podría, por ejemplo, hacer una pila de 24 monedas, una de 20, y otra de 1. Pídale que quite una moneda de cada una de sus pilas y que haga una nueva pila (en nuestro ejemplo la pila nueva tendría 3 monedas y quedarían dos pilas más de 23 y 19). Indique repetir el proceso - esto es, quitar una moneda de cada pila (incluyendo la nueva) para formar una pila nueva (lo que nos dejaría en el ejemplo con pilas de 22, 18, 3, y 2), y luego continuar repitiendo el proceso. Después de un lapso de tiempo adecuado, dependiendo de la configuración inicial y la habilidad del voluntario, usted anuncia que hay una pila de cada tamaño de 1 a 9. Nuestro problema para diciembre: probar que el truco siempre funciona. No conocemos el origen de este problema. Lo aprendimos de Igor Astapov, profesor del Royal Military College of Canada, quien a su vez lo aprendió en una página rusa de chat matemático.

Respuestas correctas:
	Recibimos respuestas correctas de  Philippe Fondanaiche (Francia) Sébastien Dumortier (Francia) Patrick LoPresti (USA)

La solución:

El problema está basado en un juego llamado Solitario Búlgaro.  Martin Gardner lo popularize en su columna, "Mathematical Games" [Scientific American 249 (Agosto 1983) pp. 18-21].  Agradecemos a  Philippe Fondanaiche por esta información. Philippe ayuda a mantener Diophante (www.diophante.fr), una página web dedicada a la recreación matemática. El Solitario Búlgaro fue su problema H101; hace poco publicaron una solución. También nos dirigió a la página http://www.augsburg.edu/math/faculty/doree/bulgarian_solitaire_bib.pdf
que contiene más de una docena de referencias que fueron inspiradas por el artículo de Gardner. Más información en el artículo de la Wikipedia http://en.wikipedia.org/wiki/Bulgarian_solitaire. 

Fondanaiche nos mandó su propia solución basada en una de las referencias. Puede verse completa en nuestra página en francés. También recibimos una solución de Sébastien Dumortier que utilize una computadora para agotar todas las posibilidades. Basó su solución en que el número de formas posibles de disponer las monedas en pilas es igual al número de particiones de 45 (o sea, la cantidad de maneras de escribir 45 como suma de enteros positivos), que son 89134 maneras. Para dar una idea, he aquí el árbol del juego para seis monedas(en vez de 450. El número 6 tienen solamente 11 particiones, por lo que el Solitario Búlgaro jugado con 6 monedas considera todos los 11 estados posibles.

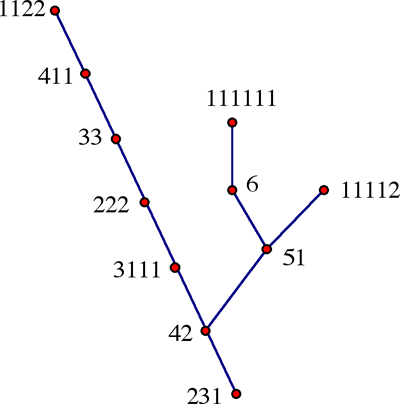
El diagrama nos dice que si comenzamos con 6 monedas en pilas de altura 1, 1, 2, y 2, entonces lleva 6 movidas llegar al estado estable con pilas de 1, 2, y 3 monedas.

Ahora presentamos la solución de Lo Presti, que hemos expandido y escrito con nueva notación. Es mucho más simple que cualquier solución que hayamos visto en papel o en internet.

La solución de LoPresti.
            Coloque las monedas en los puntos del reticulado de los enteros en el plano xy, de manera que las bases de las pilas están sobre el eje x (y=0) y la primera pila está sobre el eje y (x=0). Sea H(j) la y-coordenada de la posición de la moneda superior de la pila con base en (j,0), de manera que H(j) es la altura de la pila menos uno. Tenemos
            Pila 1: monedas en (0, 0), (0, 1), (0, 2), ..., (0, H(0))
            Pila 2: monedas en (1, 0), (1, 1), (1, 2), ..., (1, H(1))
            ...
            Pila n: monedas en (n-1, 0), (n-1, 1), (n-1, 2), ..., (n-1, H(n-1)).

            La transformación en el nuevo estado se hace así: las monedas base (0, 0), (1, 0), ..., (n, 0) en ese orden se convierten en la nueva pila 1,
(0, 0), (0, 1), ..., (0, n).
Cada moneda es desplazada una unidad a la derecha (para hacer lugar para la nueva columna) y una unidad hacia abajo (porque quitamos la moneda de la base de la pila). También puede pasar que alguna pila se vacíe mientras que las pilas a su derecha no está vacías; en ese caso se mueven hacia la izquierda algunas pilas para que no haya columnas vacías. He aquí el diagrama que obtenemos al empezar con N = 6 monedas (en vez de N = 45 como en nuestro problema):

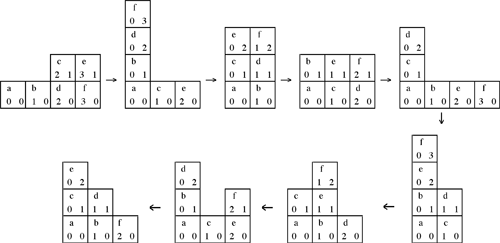
         Definimos el peso de la moneda C en la posición (x,y) como W(C)=x+y. La transformación no cambia W(C) si C es movido de (x, 0) a (0, x) o de (x, y) a (x + 1, y – 1); W(C) decrece si y solo si C está en y = 1 o más alto en una pila que es movida a la izquierda. De manera que después de algunas iteraciones todas las monedas van a haber llegado a su peso mínimo, y van a estar bajando de (0, H(C)) a (H(C), 0) de a un paso, (x, y) 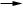(x + 1, y – 1), y después de nuevo suben a (0, H(0)).
AFIRMACION.  Una vez que todas las monedas han alcanzado su peso mínimo, si la línea x + y = k tiene al menos una moneda entonces la línea x + y = k – 1 debe contener un conjunto completo de k monedas. 
Para probar la afirmación, supongamos por el contrario que en una posición de x + y = k – 1, denotada , falta una moneda. El movimiento de C tiene período k+1, mientras que el movimiento de  tiene período k; de esta manera, en alguna movida  va a estar directamente debajo de C, contradiciendo la ley de gravedad de Newton.
            Contemos las monedas en el caso en que k = 8 es el mayor peso. Recordemos que empezamos con 45 monedas. Tenemos j+1 monedas en cada línea x + y = j desde j = 0 hasta j = 7, y a lo sumo 9 monedas en x + y = 8.  Con k = 8, tenemos 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36; se sigue que  x + y = 8 debe contener también un conjunto completo de 9 monedas para que el total sea 45.  Este arreglo, por supuesto, fuerza a la primera pila a tener 9 monedas, la siguiente 8, y así bajando hasta 1, como se buscaba.

Más comentarios.
            Con seguridad el lector habrá notado que nuestro argumento funciona para cualquier número de la forma

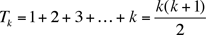
Estos son los números triangulares (T₁ = 1, T₂ = 3, T₃ = 6, ...).  Sea o no el número de monedas un número triangular, esta claro (por el hecho de que hay finitos arreglos posibles) que para cualquier arreglo de N monedas en pilas, un juego de solitario búlgaro va a terminar en un ciclo de pilas cuyos tamaños se repiten. Nuestro argumento, aplicado a un arreglo de N monedas cuando N no es triangular nos lleva a un teorema de J. Brandt ["Cycles of Partitions", Proc. Amer. Math. Soc. 85 (1982) 483-486] que describe los patrones que se repiten.

TEOREMA. Si N cumple T_k-1 < N < T_k para números triangulares consecutivos T_k-1 y T_k, entonces el arreglo de monedas se hace cíclico una vez que el número de monedas en la pila j (para j = 1, ... , k) es el de cada T_k, o sea k + 1 – j, o uno menos que ese número. Además, el número de distintos arreglos posibles en el ciclo divide a k.

Por ejemplo, si empezamos con N = 12 monedas, tenemos k = 5 (es decir, T₄ = 10 < N = 12 < T₅ = 15).  Un arreglo que se repita va a tener la primera pila con 4 o 5 monedas, la segunda con 3 o 4, la tercera con 2 o 3, la cuarta con 1 o 2 monedas, y la quinta con 0 o 1, siempre que los números sumen 12. El ciclo de cinco arreglos que contiene 5, 4, 2, 1y el ciclo de cinco arreglos que contienen 5, 3, 3, 1 producen los diez arreglos que satisfacen el teorema.

         En "Solution of the Bulgarian Solitaire Conjecture" [Math. Magazine 58:5 (November 1985) 259-271] Kiyoshi Igusa prueba que cuando N = T_k, un juego de solitario búlgaro alcanza su ciclo final en k(k – 1) movidas o menos. Puede probar la afirmación también cuando N < T_k, pero no sabe si en ese caso la estimación es óptima. No sabemos si nuestro método permite determinar estas cotas.