|
Solución del problema de Noviembre, 2007
| El problema: |
 |
PM72: Noviembre 2007
Probar que para cada n, los enteros 1, 2, 3, ..., 2n – 1, 2n pueden particionarse en pares
{a1, b1}, {a2, b2}, ..., {an, bn}
tales que ai + bi es primo para todo i.
|
Respuestas correctas: |
 |
Recibimos soluciones correctas de
Bojan Basic (Serbia) |
Wolfgang Kais (Alemania) |
Gérard Billion (Francia) |
Jeremy Lam (Reino Unido) |
Lou Cairoli (USA) |
Jacques Mertzeisen (Francia) |
John Campbell (Alberta) |
Viktor Pačnik (Eslovenia) |
Adrien Delcour (Bélgica) |
Mark Pilloff (USA) |
Philippe Fondanaiche (Francia) |
Ananda Raidu (India) |
Alenka Gabrovec (Eslovenia) |
John T. Robinson (USA) |
Xavier Hecquet (Francia) |
Heri Setiyawan (Indonesia) |
| Jean-Luc Luyet (Switzerland) |
|
|
La solución:
Comentarios preliminares. La solución depende de un resultado que es conocido como Postulado de Bertrand (por Joseph Bertrand (1822-1900) que lo conjeturó en 1845) y también como Teorema de Chebyshev (por Pafnuty Chebyshev (1821-1894) que probó la conjetura en 1850):
Para cada entero n > 1, existe al menos un número primo entre n y 2n.
O, como dijo el matemático N.J. Fine,
Chebyshev said it, but I'll say it again;
There's always a prime between n and 2n,
(que rima en inglés americano). Se pueden encontrar detalles en
http://mathworld.wolfram.com/BertrandsPostulate.html
http://en.wikipedia.org/wiki/Bertrand%27s_postulate
o en textos estándar de teoría de números.
Todos nuestros correspondentes enviaron esencialmente la misma solución. Primero veamos un ejemplo simple para motivar nuestro argumento: dividamos los números de 1 a 8 en pares, tales que la suma de cada par es prima. Hay dos primos entre 8 y 15 a los que podemos apuntar, 11 y 13. Si elegimos 13, los pares {5, 8} y {6, 7} suman 13 y usan todos los números en el subconjunto {5,6,7,8}. Hemos reducido el problema a emparejar los números de 1 a 4. Esto sugiere claramente un argumento por inducción.
Demostración por inducción. El caso n = 1 (con los enteros 1 y 2) es inmediato — los números ya forman un par cuya suma es 3, un primo. Asumamos ahora que la afirmación vale para n entre 1 y k – 1; es decir,
asumamos que para cada n entre 1 y k – 1, los enteros 1, 2, 3, ..., 2n – 1, 2n pueden particionarse en pares {a1, b1}, {a2, b2}, ..., {an, bn} tales que ai + bi es primo para todo i.
Ahora usamos la suposición para el caso n = k; es decir, tenemos que emparejar los números de 1 a 2k. Por el Postulado de Bertrand tenemos garantizado un primo entre 2k y 4k. Como
2k > p – 2k ≥ 1, podemos asociar
2k con p – 2k,
2k – 1 con p – 2k + 1,
...
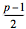 con con 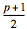 . .
Notemos que los miembros de cada par suman p, y que hemos usado todos los números entre p – 2k y 2k. Como p – 2k – 1 es un número par que es a lo sumo 2(k – 1), podemos aplicar la hipótesis inductiva para los números de 1 a p – 2k – 1, y hemos completado la demostración.
|