|
Solución del problema de Febrero, 2009
| El problema: |
 |
PM84: Febrero 2009
- Encuentre un número de 6 dígitos n = abcdef tal que defabc es igual a 6 veces n.
- Se puede hacer lo mismo con un número de 8 dígitos? (es decir, transponer los primeros cuatro dígitos con los cuatro últimos y obtener 6 veces el número original?).
|
Respuestas correctas: |
 |
Recibimos soluciones correctas de
Chris Abdnour |
Omran Kouba (Siria) |
Berkay Anahtarci (Turquía) |
Normand LaLiberté (Ontario) |
Jose Arraiz (Brasil) |
Sébastien Lebre (Francia) |
Bojan Basic (Serbia) |
Matthew Lim (USA) |
Luigi Bernardini (Italia) |
Jeff Lindstrom (Ontario) |
Lou Cairoli (USA) |
Jean-Luc Luyet (Suiza) |
Bernard Carpentier (Francia) |
Pavan Manjunan (India) |
Bernard Collignon (Francia) |
Daniel Nix (Australia) |
Olivier Cyr (Francia) |
Catherine Nadault (Francia) |
Philippe Fondanaiche (Francia) |
Shpetim Rexhepi (Macedonia) |
Baptiste Gorin (Francia) |
John T. Robinson (USA) |
Derek Graefer (Regina) |
K. Sengupta (India) |
Cornel Gruian (Rumania) |
Albert Stadler (Suiza) |
| Karim Laaouini (Marruecos) |
Benjamin Louradour (Francia) |
| Charles Huyghues Despointes (Francia) |
|
Además, James Hovious nos envió una solución informática, y hubo tres respuestas incompletes. Presentaremos primero la solución del problema y luego discutiremos las generalizaciones.
|
La solución:
Solución de la parte (a).
Sean A = abc, B = def nuestros enteros de tres dígitos que juntos forman
N = abcdef. Sabemos que 6(1000A + B) = 1000B + A; entonces
5999A = 994B.
El máximo común divisor de 994 y 5999 es 7, lo que escribimos (994, 5999) = 7. Se sigue que 857A = 142B, y como (142, 857) = 1, B debe ser múltiplo de 857. Pero B es un número de 3 dígitos, de manera que B = 857 y entonces, A = 142. Es decir, N = 142857 es el único número de 6 dígitos con la propiedad deseada:
6 × 142857 = 857142.
Comentarios. Otra forma alternative es encontrar la factorización prima de 994 y 5999, es decir 994 = 2·7·71 y 5999 = 7·857. Aunque factorizar es en general mucho más díficil que encontrar factores comunes, el problema es sencillo para una computadora si los números no son muy grandes. Agradecemos a LaLiberté por señalarnos una página web que calcula factores primos:
http://www.math.wustl.edu/primes.html.
Como discutimos abajo, muchas versiones de nuestro problema pueden ser encontradas en la literatura. Por ejemplo Cairoli encontró la parte (a) en la página de Dr. Math:
http://mathforum.org/library/drmath/view/53296.html.
Solución de la parte (b).
La repuesta es NO, no existe tal número de 8 dígitos. En forma análoga a la parte (a), sean A y B números de 4 dígitos tales que 6(10000A + B) = 10000B + A; entonces,
59999A = 9994B.
Como (9994, 59999) = 1 — de hecho 59999 es primo y 994 = 2·19·263 — deducimos que B es múltiplo de 59999. Pero queríamos que B sea un número de 4 dígitos, y entonces no hay solución.
Generalizaciones.
Varios lectores generalizaron el problema: comenzar con un número N cuya representación en base 10 tiene 2n dígitos, luego separar N en dos partes de longitud n e intercambiar las partes (sin cambiar el orden de los dígitos de cada parte); entonces el número resultante es igual a 6N si y sólo si 7 divide a 10n + 1 (o, equivalentemente, n ≡ 3 (mod 6)). Para tal valor de n,
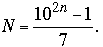
Tanto Fondanaiche como Stadler fueron un poco más lejos y mostraron que solamente multiplicando por 1 ó 6 tiene respuesta el problema. Concretamente, escribimos N = A·10n + B. Queremos determinar enteros positivos A, B, n, k tales que A y B tienen n dígitos y k·(A·10n + B) = (B·10n + A); es decir,
10n–1≤ A,B < 10n (1)
(10nk – 1)A = (10n – k)B . (2)
Deducimos inmediatamente de (1) y (2) que k ≤ 9. A continuación transcribimos la prueba de Stadler de que si k > 1, entonces necesariamente k = 6, n = 6j + 3, y
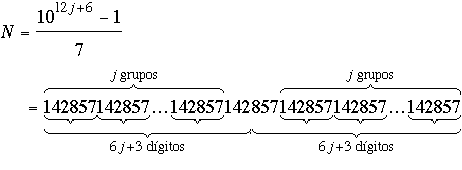
Al igual que en la primera parte donde teníamos j = 0, N = 999,999 / 7 = 142857), aquí tenemos
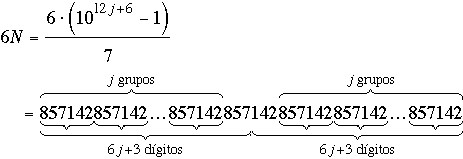
Sea d = (10nk – 1, 10n – k), el maximo común divisor de los multiplicadores de A y B en la ecuación (2). Notemos que (k –1, k + 1) es 2 ó 1 dependiendo de si k es impar o par. Con esto deducimos que
d = (10nk – 1 – k(10n – k), 10n – k) = (k2 – 1, 10n – k)
= (k – 1, 10n – k) · (k + 1, 10n – k)
= (k – 1, 10n – 1) · (k + 1, 10n + 1). (3)
Deducimos de (3) que si k = 2, 3, 5, 9, entonces d = 1. Cuando k es 4 ó 7,
d = (3, 10n – 1) = 3. Cuando k = 8: 7 divide a 10n – 1 si y solo si n es múltiplo de 6 (porque 106j = (106)j ≡ 1 (mod 7)). Entonces
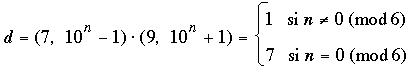
Cuando k = 6, como 1001 = 7·143,
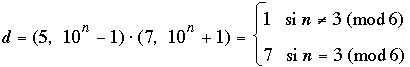
Si ponemos g = (A, B) entonces (2) es
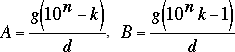
Como B debe tener n dígitos, se tiene que cumplir gk < d. Como d solo puede ser 1 ó 7 y k 6 ú 8, necesariamente g=1, y entonces k < d fuerza k = 6. La única posibilidad es entonces d = 7, k = 6, g = 1, n ≡ 3 (mod 6).
Números periódicos.
Aunque muchas respuestas mencionaron la relación de nuestro problema en la parte (a) con la fracción
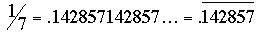 , solamente Matthew Lim explotó tal relación. Sin embargo ni siquiera él mostró cómo la relación lleva a un método que permite resolver muchos problemas. Mostremos un simple ejemplo: , solamente Matthew Lim explotó tal relación. Sin embargo ni siquiera él mostró cómo la relación lleva a un método que permite resolver muchos problemas. Mostremos un simple ejemplo:
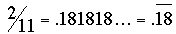 , mientras que , mientras que 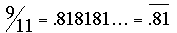
Notemos que 9/11 = (4.5) × 2/11, y de ahí el problema
Encuentre el menor entero tal que si el dígito a la izquierda del número se transfiere a la derecha del número, el nuevo número es cuatro veces y media el número original.
No sabemos cuántos dígitos usar, de manera que ponemos
N = anan–1an–2…a2a1a0 ,
tal que
9/2 N =an–1an–2…a2a1a0an .
Consideremos el número periódico
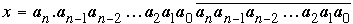
donde la parte periódica son presicamente los dígitos de N. Entonces
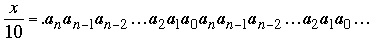
y
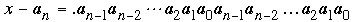
El primer número, x/10, es un número periódico donde los dígitos repetidos son los de N, mientras que el segundo número es también periódico donde los dígitos que se repiten son los de 9N/2. Se sigue que
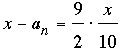
y
11x = 20an.
Queremos el menor N, y tomamos an = 1, y entonces x = 20/11 = .1818..., N = 18.
La discusión precedente se basa en The Gentle Art of Mathematics by Dan Pedoe, páginas 11-15, salvo que en su problema él usó 3/2 en lugar de 9/2 en nuestra versión simplificada.
Veamos cómo utilizar el método de Pedoe para atacar la parte (a) de nuestro problema de febrero:
Aquí N = abcdef, y ponemos x = .abcdefabcdef… , y = abc. Entonces
1000x – y = 6x,
y = 994x = 2·7·71x.
El único valor de x periódico que hace que y tenga 3 dígitos es x = 1/7. Entonces x = .142857142857…, y N = 142857.
Para practicar, intente remplazar 6 en la parte (a) por 5.5.
|