|
Solución del problema de Octubre, 2009
| El problema: |
 |
PM89: Octubre 2009
Un torneo por eliminación es una competencia que consiste en multiples rondas. En cada ronda juegan dos competidores; el ganador pasa a la siguiente ronda, y el perdedor queda eliminado. Cuando un competidor no tiene rival asignado, se le da un pase, lo que significa que pasa directamente a la siguiente ronda. Nos interesa saber cuál es el mínimo número de pases en un torneo que tiene n competidores. Por ejemplo, cuando hay 6 participantes, el torneo puede tener dos pases en la primera ronda, o puede no tener pases en la primera ronda y tener uno en la segunda; entonces el mínimo número de pases para un torneo de 6 competidores es uno.
- ¿Cuál es el número mínimo de pases en un torneo por eliminación con 2010 participantes?
- Por diversos problemas solamente pudieron competir 1025 participantes. ¿Cuántos pases debe haber en el nuevo cuadro?
|
Respuestas correctas: |
 |
Recibimos soluciones correctas de
Claudio Baiocchi (Italia) |
Omran Kouba (Siria) |
Halima Abdalla Bashier (Regina) |
Tannie Lau |
Bojan Basic (Serbia) |
Matthew Lim (USA) |
José Borges (Portugal) |
Jeff Lindstrom (Ontario) |
Lou Cairoli (USA) |
John T. Robinson (USA) |
Dan Dima (Rumania) |
Uwe Schaefer (Alemania) |
Sébastien Dumortier (Francia) |
Nutheti Shivdeep (India) |
Magnus Jakobsson (Suecia) |
Albert Stadler (Suiza) |
|
La solución:
Parece casi obvio que para obtener el número mínimo de pases en un torneo deberemos tener exactamente un pase en cualquier ronda con número impar de participantes, y ninguno en rondas con número par de participantes. Por otro lado, como el número de pases en una ronda afecta la cantidad de participantes en la siguiente, parece posible que pases extras en una ronda produzcan ahorros más adelante. Pero no es así: utilizar más que el mínimo de pases en una ronda siempre incrementa el número total de pases. En efecto, si la ronda r tiene un número par de participantes c, el número de pases en esa ronda, digamos b, también será par, el número de participantes que pasan a la ronda r + 1 será 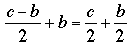 . Si tanto c/2 como b/2 son impares (lo que implica b ≥ 2), entonces no habría pases en esa ronda, lo que representa un ahorro de a lo sumo un pase en la ronda r + 1; pero hubo por lo menos dos pases de más en la ronda r de manera que el número total de pases aumenta. Entonces, para ronda con número par de participantes, usar más de b = 0 pases incrementa el número de pases en el torneo. Un argumento similar lleva a la misma conclusión cuando el número de participantes es impar (donde el número de pases será necesariamente impar). Mostraremos un argumento alternativo al final, pero coincidamos por ahora en que . Si tanto c/2 como b/2 son impares (lo que implica b ≥ 2), entonces no habría pases en esa ronda, lo que representa un ahorro de a lo sumo un pase en la ronda r + 1; pero hubo por lo menos dos pases de más en la ronda r de manera que el número total de pases aumenta. Entonces, para ronda con número par de participantes, usar más de b = 0 pases incrementa el número de pases en el torneo. Un argumento similar lleva a la misma conclusión cuando el número de participantes es impar (donde el número de pases será necesariamente impar). Mostraremos un argumento alternativo al final, pero coincidamos por ahora en que
Cuando hay c participantes en una ronda y c es par, entonces no habrá pases en esa ronda y c/2 participantes pasarán a la ronda siguiente; cuando c es impar habrá un pase en esa ronda y (c + 1)/2 participantes pasarán a la siguiente ronda.
Se sigue que el número mínimo para el torneo por eliminación con 2010 participantes sera de 3 pases ; en cada ronda el número será
2010, 1005, 503, 252, 126, 63, 32, 16, 8, 4, 2.
Hemos marcado las tres rondas en las que hay pase. De modo similar, habrá 10 pases cuando el torneo comience con 1025 participantes, un pase en cada ronda hasta llegar a la última. El número de participantes en cada ronda será
1025, 513, 257, 129, 65, 33, 17, 9, 5, 3, 2.
La mayoría de las respuestas notaron la conexión entre la regla para encontrar en número mínimo de pases y el algoritmo para convertir un número de base-10 a binario. Resulta que el número mínimo de pases en un torneo con n participantes es igual a la cantidad de ceros de la representación de n – 1 en base 2. Dima y Robinson citaron la enciclopedia de sucesiones de enteros,
http://www.research.att.com/~njas/sequences/A080791.
Lamentablemente no hay explicación en la página web. Una manera más agradable de calcular este número es tomar h como el menor entero tal que 2h ≥ n. Entonces
El número mínimo de pases en un torneo con n participantes es igual al número de unos en la representación de 2h – n en base 2.
Por supuesto que ambas reglas producen el mismo resultado: 2h – 1 es un número cuya representación en base 2 consiste de todos unos, de manera que 2h – n = 2h – 1 – (n – 1) es un número binario que tiene un uno precisamente en la posiciones donde (n – 1)2 tiene un cero. Por ejemplo
2010 – 1 = 2009 = 111110110012tiene tres 0s;
211 – 2010 = 2048 – 2010 = 38 = 1001102tiene tres 1s..
Kouba mostró otros ejemplos simples:
| para n |
= 2k |
número de pases es |
0, |
| |
= 2k – 1 |
|
1, |
| |
= 2k + 1 |
|
k. |
Para mostrar por qué funciona esta regla combinaremos los argumentos de Jakobsson y Dumortier con ideas de Baiocchi, Cairoli y Kouba. Introducimos la noción de participante imaginario (por oposición a real) para redondear el número de participantes a la potencia de dos inmediata siguiente. Los participantes imaginarios juegan partidos imaginarios: el número de partidos en un torneo con n participantes es n-1 (porque todos salvo el campeón pierden una vez). Recordemos que h es el menor entero tal que 2h ≥ n. Definimos
Cr el número de participantes reales en la ronda r (o sea que C1 = n),
Ir = 2h–r+1 – Cr el número de participantes imaginarios en la ronda r,
Mr el número de partidos reales en la ronda r,
IMr el número de partidos imaginarios jugados entre jugadores imaginarios,
Hr el número de partidos híbridos (entre participante real e imaginario).
He aquí los números para el torneo con n = 2010 participantes utilizando la regla de que en cada ronda hay a lo sumo un partido híbrido.
r |
Cr |
Ir |
Mr |
IMr |
Hr |
1 |
2010 |
38 |
1005 |
19 |
0 |
2 |
1005 |
19 |
502 |
9 |
1 |
3 |
503 |
9 |
251 |
4 |
1 |
4 |
252 |
4 |
126 |
2 |
0 |
5 |
126 |
2 |
63 |
1 |
0 |
6 |
63 |
1 |
31 |
0 |
1 |
7 |
32 |
0 |
16 |
0 |
0 |
8 |
16 |
0 |
8 |
0 |
0 |
9 |
8 |
0 |
4 |
0 |
0 |
10 |
4 |
0 |
2 |
0 |
0 |
11 |
2 |
0 |
1 |
0 |
0 |
Asumimos que en los partidos híbridos siempre gana el participante real; en ese caso Hr representa el número de pases en la ronda r. El número de participantes en la siguiente ronda satisface
Cr+1 = Hr + Mr.
Este es el argumento prometido más arriba: para mantener el total en la columna Hr ta pequeño como se pueda, ponemos un partido híbrido solamente cuando es necesario: el número de partidos híbridos en cada ronda es igual al número total al número total de partidos de la ronda restado de 2h–r (donde 2h–r es la mitad del número total de participantes reales e imaginarios en la ronda). Por lo tanto el número de partidos Mr + IMr + Hr = 2h–r de cada ronda: si Mr decrece en k, también IMr, y Hr se incrementa en 2k. Como el total en la columna Mr siempre es uno menos que el total de participantes, tenemos que para obtener el número mínimo de pases tenemos que maximizar el número de partidos imaginarios; esto es, Hr a lo sumo 1 para cada r.
Para llenar la tabla de arriba, comenzamos con C1 = 2010 y h = 11; luego, I1 = 211 – 2010 = 38. Cuando Cr es par, el número de partidos satisface 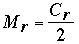 ; cuando Cr es impar, , ; cuando Cr es impar, , 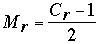 . En cualquier caso, Cr+1 = Cr – Mr (es decir, un participante es eliminado después de cada partido). Para los participantes imaginarios (cuyo número – por definición – tiene la misma paridad que Cr) tenemos fórmulas análogas: IMr = . En cualquier caso, Cr+1 = Cr – Mr (es decir, un participante es eliminado después de cada partido). Para los participantes imaginarios (cuyo número – por definición – tiene la misma paridad que Cr) tenemos fórmulas análogas: IMr =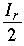 ó ó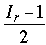
según Ir sea par o impar.
La tabla debería dejar en claro cómo el número de pases (que es la suma de los números en la columna Hr) se relaciona con la representación binaria de I1 = 2h – C1. En efecto, la columna Hr nos da los dígitos de I1 en orden inverso (comenzando con las unidades): 38 = 1001102. En general, Ir dividido por 2 es igual a Ir+1 con resto Hr, de maner que Hr es le dígito en la posición 2r–1 de la representación binaria de I1.
Comentario adicional. No está claro que haya alguna ventaja en particular en desarrollar un torneo que tenga el mínimo posible de pases. La mayoría de los torneos se organizan d manera que todos los pases estén en la primera ronda (en el lenguaje de arriba, esto es decir que cada jugador imaginario juega contra un jugador real en la primera ronda, de manera que hay Ir partidos híbridos en la primera ronda y ninguno en las demás). De esta manera los organizadores controlan quiénes reciben los pases. Tal vez es más justo tener el número mínimo de pases en el sentido de que minimiza la cantidad de veces en que se enfrentan participantes que han jugado un número diferente de partidos.
|