|
Solución del problema de Septiembre, 2009
| El problema: |
 |
PM88: Septiembre 2009
La función f(x) satisface dos propiedades:
(i) f(x + y) + f(x - y) = 2[f(x) + f(y)];
(ii) f(1) = 1.
¿Cuánto vale f(22/7)?
|
Respuestas correctas: |
 |
Recibimos soluciones correctas de
Aditya Prasad
|
Cornel Gruian (Rumania) |
Roopesh Mangal (India) |
Bojan Basic (Serbia) |
Gustavo Krimker (Regina) |
Anónimo |
Lou Cairoli (USA) |
Omran Kouba (Siria) |
Mark Pilloff (USA) |
Olivier Cyr (Francia) |
Jinzhong Li (China) |
John T. Robinson (USA) |
Allen Druze (USA) |
Matthew Lim (USA) |
Nutheti Shivdeep |
Milan Pavic (Serbia) |
Jeff Lindstrom (Ontario) |
Albert Stadler (Suiza) |
Federico Felizzi (Italia) |
Patrick LoPresti (USA) |
A. Teitelman (Israel) |
Normand LaLiberté
(Ontario) |
Philippe Fondanaiche
(Francia) |
José António Nunes
Borges (Portugal) |
Bernard Collignon
(Francia) |
Berkay Anahtarci
(Turquía) |
Karim Laaouini
(Marruecos) |
Claudio Baiocchi
(Italia) |
Bruce Gilligan
(Regina) |
|
Recibimos además dos soluciones incompletas y una incorrecta.
|
La solución:
Es fácil adivinar que la respuesta es 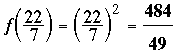 .
Una manera es utilizar las propiedades dadas para determinar el valor de f(x) para valores pequeños de x: .
Una manera es utilizar las propiedades dadas para determinar el valor de f(x) para valores pequeños de x:
Si x = y = 0 entonces f(0) + f(0) = 2[f(0) + f(0)], luego 2f(0) = 4f(0), y f(0) = 0.
Si x = y = 1 entonces f(2) + f(0) = 2[f(1) + f(1)] = 4, de donde f(2) = 4.
Si x = 2, y = 1 entonces f(3) + f(1) = 2[f(2) + f(1)]; utilizando los valores ya sabidos de f deducimos que f(3) + 1 = 2[4 + 1], ó f(3) = 9.
¡Aparece un patron! La mayoría de las respuestas utilizaron este patrón para obtener la respuesta directamente (usando aritmética elemental) o utilizaron inducción para obtener un resultado más general. Presentamos ambos métodos.
El método directo. Presentamos una síntesis de las soluciones de Li y Pavic. Ya hemos visto que f(0) = 0. Para cualquier número real x, si ponemos y = x en (i) tenemos
f(2x) + f(0) = 2(f(x) + f(x)) = 4 f(x), de donde
f(2x) = 4 f(x).
Se sigue que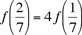 and and 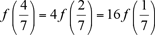 . .
Con x = 2/7, y = 1/7, deducimos que 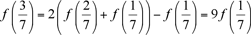 ; ;
luego, con x = 4/7, y = 3/7, tenemos
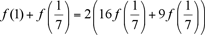 , de manera que , de manera que 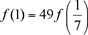 , y entonces, , y entonces,
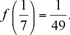
Poniendo x = 1, y = 4/7, deducimos 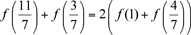 que implica que implica
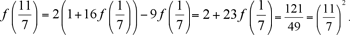
Finalmente,
como se afirmaba.
Inducción matemática. Este es el camino elegido por la mayoría. Combinamos sus demostraciones de que para todo real r y enteros m,n las condiciones (i) y (ii) implican
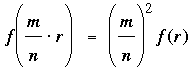
Probamos primero que f(m·r) = m2 f(r) para enteros positivos m:
Ya vimos que f(0·r) = 0 = 02r, y – trivialmente – que f(1·r) = 12f(r). Suponiendo que f(k·r) = k2f(r) para k desde 1 hasta m, probaremos que vale para m + 1. Si x = mr, y = r obtenemos f((m + 1)r) + f((m – 1)r) = 2[f(mr) + f(r)], y por la hipótesis inductiva tenemos f((m + 1)r) + (m – 1)2f(r) = 2[m2f(r) + f(r)], ó
f((m + 1)r) = [2m2 + 2 – (m2– 2m + 1)]f(r) = (m + 1)2f(r),
lo que prueba que f(m·r) = m2f(r) para todos los enteros positivos.
El resultado se extiende fácilmente a los enteros negativos: para todo número real s, poniendo x = 0, y = s tenemos f(s) + f(–s) = 2[0 + f(s)], lo que implica que f(s) = f(–s); luego, f(m·r) = m2f(r) para todo entero m y número real r.
Finalmente, escribiendo m·r como n·mr/n (con n un entero no nulo) en el resultado anterior obtenemos m2f(r) = f(m·r) = f(n·m·r/n) = n2f(m·r/n), y se deduce
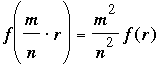
como se quería.
Nuestro problema es el caso especial r = 1, m = 22, n = 7: f(22/7) = (22/7)2.
Comentarios. Los requisitos (i) y (ii) en f(x) no restringen el valor de f cuando x es irracional. Por ejemplo el número π (el radio de la circunferencia de un círculo por su diámetro) está cerca de 22/7, pero se sabe que π no puede alcanzarse desde 1 en un número finito de pasos usando sumas, diferencias, productos y cocientes como hicimos con 22/7; le podemos asignar un valor arbitrario a f(π) sin violar (i) or (ii). En otras palabras, para extender nuestro resultado de que f(x) = x2 a todos los números reales, debemos postular alguna propiedad adicional, como por ejemplo continuidad. Es sencillo probar que la única función continua que cumple (i) y (ii) es la función f(x) = x2. En su solución, Mangal supuso que f(x) es diferenciable para todo x; probó entonces que se sigue inmediatamente de (i) que f '(x)
satisface la ecuación funcional de Cauchy (que discutimos a continuación).
La propiedad (i) es un ejemplo de ecuación functional: esto es, una ecuación en que la indeterminada es una función. Las ecuaciones funcionales aparecen naturalmente en muchas aplicaciones, y fueron estudiadas por primera vez en el siglo 18 para resolver problemas físicos. El primer estudio sistemático fue el de Cauchy en su famoso tratado Course d'analyse de l'École Polytechnique, publicado in 1821. Allí estudió lo que actualmente se conoce como las cuatro ecuaciones fundamentals de Cauchy; la más conocida es f(x + y) = f(x) + f(y), cuya única solución continua es f(x) = kx para alguna constante k. La historia puede encontrase en libros introductorios sobre ecuaciones funcionales como
J. Aczel, Lectures on Functional Equations and their Applications (Academic Press, 1966).
Wikipedia tiene también información en "Cauchy functional equation":
http://en.wikipedia.org/wiki/Cauchy%27s_functional_equation.
Tanto Matthew Lim como Aditya Prasad estudiaron el problema de determiner la funnción más general que cumple (i) y (ii). Para ello se necesita el concepto de una base de Hamel H: un conjunto de números reales tales que para todo número real r hay un único subconjunto finito {r1,…,rn} de H y racionales qj tales que
r = q1r1 + q2r2 + ... + qnrn.
De hecho Hamel desarrolló el concepto en 1905 para responder a la pregunta análoga sobre la ecuación funcional de Cauchy. La construcción de una base de Hamel no es para nada trivial: require el Axioma de Elección. Para nuestra ecuación funcional Lim y Prasad encontraron que para dos número u, v en la base de Hamel se pueden asignar arbitrariamente los valores f(u), f(v), f(u + v). (En nuestro problema asignamos arbitrariamente el valor f(1) = 1 para hacer único nuestro problema. Si hubiéramos querido, podríamos haber remplazado (ii) con f(√2) = 2009, y pedido el valor de f((22√2)/7), que es 2009·(22/7)2 gracias a la segunda solución mostrada). Para aquellos interesados en los detalles, agregamos un link al argumento de Lim.
|