|
Solución del problema de Abril, 2011
| El problema: |
 |
- ¿Existe una función continua $f: \mathbb{ R}\rightarrow \mathbb{ R}\;$ que tome cada uno de sus valores exactamente dos veces?
- ¿Existe una función continua $f: \mathbb{ R}\rightarrow \mathbb{ R}\;$ que tome cada uno de sus valores exactamente tres veces?
Respuesta.
No para (a); Sí para (b).
|
Respuestas correctas: |
 |
Recibimos soluciones correctas de
| Lou Cairoli (USA) |
Mei-Hui Fang (Austria) |
| Philippe Fondanaiche (Francia) |
Gruian Cornel (Rumania) |
| Tom Holens (Manitoba) |
Lars Huettenberger (Alemania) |
| Benoît Humbert (Francia) |
Ile Ilijevski (Macedonia) |
| Kipp Johnson (USA) |
Omran Kouba (Siria) |
| Antek Łączkowski (Polonia) |
Matthew Lim (USA) |
| Patrick J. LoPresti (USA) |
Fatemeh Naghipour (Regina) |
| Paolo Perfetti (Italia) |
Shpetim Rexhepi (Macedonia) |
| John T. Robinson (USA) |
Ignacio Somma Esteves |
| Albert Stadler (Suiza) |
|
Tres respuestas tenÌan la idea correcta para (b) pero cometieron un pequeño error en la ecuación. Hubo una solución incorrecta.
|
La solución:
Solución parte (a).
Comentarios preliminares. Nuestro argumento se basa en dos resultados fundamentales sobre la recta real::
Teorema de los Valores Extremos. Si $f(x)$ es una función continua a valores reales para $a \le x \le b$, y $r$ es cualquier número entre $f(a)$ y $f(b)$, entonces existe un número $c$ entre $a$ y $b$ tal que $f(c) = r$. (Este teorema representa la noción intuitiva de que uno puede dibujar una función continua sin
levantar el lápiz de la hoja).
The Extreme Value Theorem. Si $f(x)$ es una función continua a valores reales para
$a \le x \le b$, entonces alcanza su máximo y su mÌnimo en el intervalo. (Es decir, existen $c$ y $d$ en el cerrado $[a,b]$ tales que $f(c) \leq f(x) \le f(d)$ para todo $a \le x \le b$.)
Los matemáticos utilizaron estos teoremas implÌcitamente durante siglos, pensando que eran resultados obvios. Pero fueron formulados (y demostrados) correctamente recién en el siglo XIX.
Perfetti encontró nuestro problema como el número $1.3.22$ en la página 17 de Problems in Mathematical Analysis II, Continuity and Differentiation, por W.J. Kaczor y M.T. Nowak, publicado por la American Mathematical Society (2001).
Todas las respuestas recibidas eran similares; nuestro argumento ha sido tomado mayormente de Patrick LoPresti, con algunas ideas adicionales de otros lectores.
Prueba de no-existencia.
Supongamos que existe $f(x)$ que toma todos los valores de su rango exactamente dos veces. Tomemos $r$ en su rango. Sin perder generalidad, supondremos que $r=0$ (la función $g(x) =f(x)-r$ toma todos sus valores exactamente dos veces si y solo si $f(x)$ lo hace). Suponemos entonces que $f(x)=0$ para exactamente dos valores de $x$, digamos $a$, $b$; es decir, $f(a) = f(b) = 0$ y $f$ es no-nula para todos los demás $x$.
Consideremos el comportamiento de $f(x)$ cuando $a<x<b$. Para tales $x$, la función $f(x)$ debe ser totalmente positiva o totalmente negativa; porque si cambia de signo entre $a$ y $b$, por el Teorema de los Valores Intermedios deberÌa haber un cero de la función entre $a$ y $b$, contradiciendo el hecho de que $a$ y $b$ son los únicos dos ceros. Supondremos entonces que $f(x)>0$ para todo $x$ tal que $a<x<b$ (si $f(x)$ es negativa, podemos trabajar con la función $-f(x)$).
Por el Teorema de los Valores Extremos, $f(x)$ alcanza su máximo, digamos $M$: $f(c) = M$ para algún $c$ tal que $a \le c \le b$. De hecho, como $f(x)$ es cero en $a$ y en $b$, y positiva en entremedio, $M>0$ y se desprende que $a < c < b$. Por hipótesis, existe exactamente otro valor de $x$, digamos $x=d \ne c$, tal que $f(x) = M$. ¿Dónde está tal $d$?
Supongamos $d > b$. Entonces $$a < c < b < d, \quad f(a) = 0, f(c) = M, f(b) =0, \mbox{ y } f(d) = M.$$ Por el Teorema de los Valores Intermedios, $f(x)$ debe tomar todos los valores entre $0$ y $M$ cuando $x$ va desde $a$ hasta $c$, y de nuevo cuando $x$ va desde $c$ hasta $b$; y una tercera vez cuando $x$ va desde $b$ hasta $d$. Entonces $f(x)$ estarÌa tomando cada uno de sus valores al menos tres veces, contradicción. Entonces $d\leq b$.
Mediante un razonamiento similar, $d\geq a$. Como además $f(d)=M>0$, $d\ne a$, $d\ne b$, es decir $a<d<b$. Cambiando los roles de $c$ y $d$ si es necesario, podemos suponer que $c < d$. Por definición, $M$ es el máximo de $f(x)$ para $x$ entre $a$ y $b$; en particular, entre $x=c$ y $x=d$, $f(x) \le M$. Como $f(x)$ toma sus valores dos veces y no más, $f(x)<M$ para todo $x$ entre $c$ y $d$. Pero esto genera una contradicción, porque ya habÌamos establecido que $f(x)$ tomaba todos sus valores de $0$ a $M$ entre $a$ y $c$, y entre $d$ y $b$. ConcluÌmos que no hay ubicación posible para $d$, y entonces es imposible que $f(x)$ tome todos sus valores exactamente dos veces.
Comentario. Fang, Fondanaiche, Humbert, y LoPresti notaron que, más generalmente,
no existe ninguna función continua que tome todos sus valores exactamente $n$ veces si $n$ es par. Esto se puede ver utilizando las mismas ideas expuestas arriba.
Solución a la parte (b). Los ejemplos que recibimos de funciones continuas que toman sus valores exactamente tres veces vinieron en tres tipos:
Tipo 1.
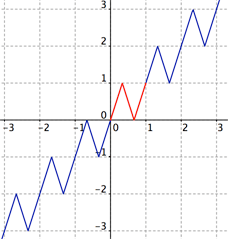 |
para cada entero $k$, sea
$$\small f(x) = \left\{
\begin{array}{lcc}
3(x-k) + k & 0 \le x-k \le \frac13 \\
-3(x-k)+2+k & \frac13 \le x-k \le \frac23 \\
3(x-k) -2+k & \frac23 \le x-k \le 1
\end{array}
\right ..$$ |
Figura 1: f(x)
La Figura 1 es una pequeña modificación del fichero de GeoGebra que recibimos de Benoít Humbert. GeoGebra, como implica su nombre, combina gráficos con álgebra. Este software puede ser descargado gratuitamente, pero cuesta un poco entender cómo utilizarlo.
Tipo 2.
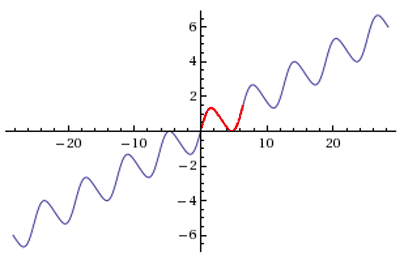
Figura 2: $g(x) = \frac2{3\pi}x + \sin x +\frac1{3\pi}\sin 2\pi$
La Figura 2 es una copia de la página de WolframAlpha producida por Patrick LoPresti, que obtuvo al introducir
graph[2/(3pi)*x + sin(x) + 1/(3pi)*sin(2x)]
en la página www.wolframalpha.com. En tal página se puede explorar el gráfico
y también modificar la ecuación.
Tipo 3.
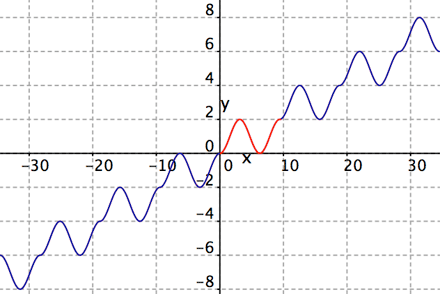
Figure 3: para cada entero $k$, sea
$h(x) = (2k+1)- (-1)^k\cos x$, for $3k\pi \le x \le 3(k+1)\pi$.
Cada una de la tres figuras muestra claramente una función que toma todos los valores reales exactamente tres veces. Los extremos relativos de cada curva están espaciados regularmente y hay un patrón básico que se repite. Cada uno de estos patrones toma sus valores tres veces, excepto por el primero y el último. El valor inicial aparece dos veces en el patrón, pero aparece una vez más como máximo relativo en el patrón anterior a la izquierda. Esto se puede confirmar algebraicamente utilizando las fórmulas que acompaÒan la primera y tercer figuras. La segunda es algo más complicada: hay que verificar que la derivada de $g(x)$ es cero en todos los múltiplos impares de $\frac\pi2$, y que
$$g\left(\frac{(4k+1)\pi}2\right) = g\left(\frac{(4k+7)\pi}2\right)=\frac43(k+1) \mbox{ para todo entero } k.$$
Más comentarios. DeberÌa estar claro, más generalmente, que existe una función continua a valores reales que toma cada valor de su rango exactamente $n$ veces si y solo si $n$ es impar} En efecto, cualquier para cualquier entero positivo impar se puede moficiar cualquiera de las tres figuras para producir funciones continuas que toman sus valores exactamente $n$ veces: simplemente hay que considerar patrones básicos con $n-1$ puntos extremos. Algebraicamente, la ecuación para $h(x)$ se convierte en $$h_n(x) = (2k+1)- (-1)^k\cos x, \; \mbox{ para }\; nk\pi \le x \le n(k+1)\pi.$$
La Figura 4 muestra el caso $n=5$. Compare con la función general $g_n(x) = \frac2{n\pi}x + \sin x +\frac1{n\pi}\sin 2x$ que se muestra (para $n=5$) en la Figura 5.
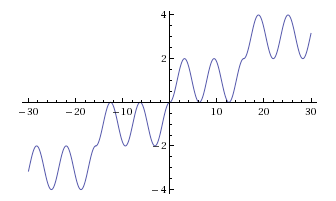
Figura 4: $h_5(x)$ toma todo valor real exactamente 5 veces.
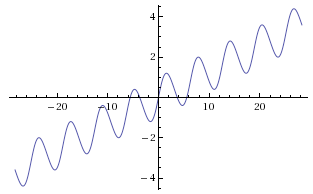
Figura 5: $g_5(x) = \frac2{5\pi}x + \sin x +\frac1{5\pi}\sin 2x$ toma todo valor real exactamente 5 veces
También debe estar claro que cualquier intervalo abierto, finito o infinito, puede
servir como rango de una función continua que toma sus valores exactamente $n$ veces cuando $n$ es impar: simplemente hay que encoger la amplitud de cada patrón fundamental. Cuando $n=3$, por ejemplo, para encoger el rango de $h(x)$ a
$-1< y < 1$, definimos en cada intervalo $3k\pi \le x \le 3(k+1)\pi$, $k = 0, 1, 2, \dots$, $h(x) = \frac{2^k-1}{2^k} + \frac1{2^{k+2}}(1- (-1)^k\cos x)$; extendemos la curva hacia la izquierda definiendo $h(-x) = -h(x)$. En la Figura 6 mostramos la parte derecha de la función.
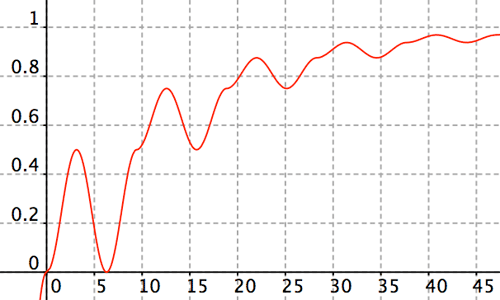
Figura 6: El rango de $y=h(x)$ para $x\geq0$ es $0\leq y<1$
|