Solución del problema de Marzo, 2011

El problema:

El problema de este mes es nuestro tributo a Jorge Luis Borges, autor de La Biblioteca de Babel. La Enciclopedia Cabalística de Permutaciones del Alfabeto consiste de siete volúmenes con las permutaciones del alfabeto de 26 letras en orden alfabético. Los volúmenes son muy grandes y están escritos en letra muy pequeña, debido a que hay tantas permutaciones. Cada volumen contiene exactamente un séptimo del total de permutaciones; si se abre el primer volumen y se mira con una lupa, se ve en el tope la primera permutación abcdefghijklmnopqrstuvwxyz, seguida por abcdefghijklmnopqrstuvwxzy. El problema: ¿cuál es la última permutación que aparece en el primer volumen? Respuesta. dswoeczyxvutrqpnmlkjihgfba.

Respuestas correctas:

Recibimos soluciones correctas de Luigi Bernardini (Italia) Daniel Bitin Lou Cairoli (USA) Bernard Collignon (Francia) Mei-Hui Fang (Austria) Philippe Fondanaiche (Francia) Gruian Cornel (Rumania) Tom Holens (Manitoba) Benoît Humbert (Francia) Ile Ilijevski (Macedonia) Kipp Johnson (USA) Wolfgang Kais (Alemania) Antek Łączkowski (Polonia) Matthew Lim (USA) Patrick J. LoPresti (USA) M.C. Juan Mir Pieras (España) John T. Robinson (USA) Dustin Sawatzky Mathias Schenker (Suiza) Albert Stadler (Suiza) Hakan Summakoğlu (Turquía) Paul Voyer (Francia)

La solución:

Cada volumen contiene exactamente $\frac17 \times 26! = 26 \times 25 \times 24\times 23\times22\times3\times20!$ permutaciones. Como 7 divide a $\frac{26!}{20!}$, la tarea se reduce a determinar las primeras seis letras de la última permutación del primer volumen: todas las $20!$ permutaciones que comienzan con esas seis letras aparecen juntas al final del primer volumen, y esa última permutación -- que comienza con las seis letras a determinar -- tendrá sus últimas 20 letras iguales a las restantes letras del alfabeto en orden alfabético invertido.

La solución entonces proviene de la simple observación de que las 26! permutaciones están organizadas en 26 bloques de igual tamaño. El primer bloque contiene todas las 25! permutaciones que comienzan con la letra $a$; ese bloque es seguido por las 25! permutaciones que comienzan con $b$, y asÌ siguiendo hasta las 25! permutaciones que comienzan con $z$ (si esto no es obvio para el lector, le sugerimos intentar, como ejercicio preliminar, organizar alfabéticamente las $4! = 24$ permutaciones de las letras $abcd$ en tres columnas, cada una con ocho filas). El primer volumen contiene $1/7$ de esos bloques: como $\frac{26}7 = 3 + \frac57$, contiene enteros los bloques que comienzan con las letras $a, b$, $c$, y $\frac57$ del bloque que comienza con $d$.

Las 25! permutaciones que comienzan con $d$ están organizadas en bloques de longitud $24!,$, cada uno comenzando con una letras distinta que $d$. Como $\frac57 \times 25 = 17 + \frac67$, el último bloque del primer volumen comienza con la

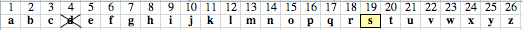
18$^a$ letra del alfabeto sin contar $d$, es decir $s$. Encontraremos nuestra tercera letra $\frac67$ del camino en la lista de permutaciones que comienzan con $ds$. El patrón deberÌa estar claro: estamos expandiendo la fracción $26! / 7$ de una
manera peculiar,
$$\frac{26!}7 = 3\cdot 25! + 17\cdot 24! + 20 \cdot 23! + 13\cdot22!+3\cdot21! + 3\cdot 20!,$$
que se explica mediante la siguiente tabla:

\[ \begin{array}{lll} \frac 47 \cdot 23 = 13 + \frac 17 & \quad \frac 17 \cdot 22 = 3 + \frac17 & \quad \frac17 \cdot 21 = 3 \\ \frac 47 \cdot 23 = 13 + \frac 17 & \quad \frac 17 \cdot 22 = 3 + \frac17 &\quad \frac17 \cdot 21 = 3\end{array}\]

Entonces, tras determinar que las primeras dos letras de la permutación buscada son $ds$, avanzamos $20\cdot23!$ permutaciones para encontrar que la tercera letra será la $20 + 1 = 21^{\rm a}$ entre las letras restantes, es decir $w$; las letras restantes son
abcefghijklmnopqrtuvxyz. Luego $13\cdot22!$ permutaciones más para determinar que la cuarta letras es la $14^{\rm a}$ de las restantes $23$, es decir $o$. Luego $3\cdot 21!$ permutaciones más para encontrar que la quinta letra es la cuarta, es decir $e$, seguida de $3\cdot 20!$ permutaciones para encontrar que la sexta letra es $f$. Las letras restantes son abcghijklmnpqrtuvxyz; como ya se mencionó, buscamos la última palabra de todas las que empiezan con dswoef, de modo que estas letras restantes aparecerán en orden alfabético inverso.

Comentarios. Varios lectores notaron que la solución de nuestro problema recuerda el proceso de convertir un número de base 10 a otra base. De hecho, cada entero menor que $(n+1)!$ tiene una representación única $$a_nn! + a_{n-1}(n-1)! + \dots + a_1(1!) + a_0(0!)\;,$$ donde $a_k$ es un entero, $0 \le a_k \le k$ para todo $k = 0, \dots , n$. Este número puede denotarse $$a_na_{n-1}\dots a_10_!,$$ donde el subÌndice factorial sugiere la relación entre esta representación y la representación en una base fija. Por ejemplo, $13 = 2010_! = 2\cdot3! + 0\cdot 2! + 1\cdot 1! + 0 \cdot 0!$, mientras que la permutación de nuestro problema --- la última permutación del volumen 1 --- aparecerÌa como la permutación número $3[17][20][13]3300\dots0_!$, que termina en $20$ ceros (y los corchetes indican que los números que encierran son considerados como dÌgitos). Pueden encontrarse detalles, entre otros lugares, en este artÌculo de Wikipedia: http://en.wikipedia.org/wiki/Factorial_number_system. Varios lectores desarrollaron sus propios programas de computadora para convertir el número factorial en la permutación correspondiente.
Tanto Schenker como Kais mostraron la primera y última permutación de cada volumen. IncluÌmos la lista para que cada lector pueda testear su propio algoritmo.

\[ \begin{array}{ccc}
\hline
% after \\ : \hline or \cline{col1-col2} \cline{col3-col4} ...
\mbox{Volumen} & \mbox{Primera Permutación} & \mbox{ ⁄ltima Permutación} \\
\hline
1 & \mbox{abcdefghijklmnopqrstuvwxyz} &\mbox{dswoeczyxvutrqpnmlkjihgfba} \\
2 & \mbox{dswoefabcghijklmnpqrtuvxyz} &\mbox{hltdigzyxwvusrqponmkjfecba}\\
3 & \mbox{hltdijabcefgkmnopqrsuvwxyz} &\mbox{ldptkjzyxwvusrqonmihgfecba}\\
4 & \mbox{ldptkmabcefghijnoqrsuvwxyz} &\mbox{owkgpnzyxvutsrqmljihfedcba}\\
5 & \mbox{owkgpqabcdefhijlmnrstuvxyz} &\mbox{sogwrqzyxvutpnmlkjihfedcba}\\
6 & \mbox{sogwrtabcdefhijklmnpquvxyz} &\mbox{whdlvuzyxtsrqponmkjigfecba}\\
7 & \mbox{whdlvxabcefgijkmnopqrstuyz} &\mbox{zyxwvutsrqponmlkjihgfedcba}\\
\hline
\end{array} \]

Lou Cairoli nos menciona un lindo libro de matemática recreativa relacionado con el problema de este mes: William Goldbloom Block, The Unimaginable Mathematics of Borges' Library of Babel, Oxford University Press, 2008.

Kipp Johnson produjo la solución más sencilla del problema: compró la Enciclopedia CabalÌstica en amazon.com y miró la última página. Nos deja perplejos que la Enciclopedia ya no se consigue, mientras que libros como el Diccionario Webster se venden bien, aún cuando contienen muchas menos palabras y permiten
repeticiones.

Hablando de perplejidad, Albert Stadler encontró las permutaciones (en inglés)

• Blowzy night-frumps vex'd Jack Q. and
  
  
• Glum Schwartzkopf vex'd by NJ IQ.

en la Enciclopedia. Nos cuenta que cada volumen de su copia de la enciclopedia tiene exactamente un millón de páginas, y desafÌa a los lectores a determinar las páginas en que aparecen estas permutaciones (¡por favor enviar las soluciones a Albert, no a nosotros!). Mientras, Cairoli nos informa que las oraciones utilizando todas las letras del alfabeto son llamadas pangramas (u oraciones holoalfabéticas, si uno es suficientemente
pedante) y nos muestra la permutación número 196307974427380973351813573 como ejemplo minimal:

Mr. Jock, TV quiz PhD, bags few lynx.

Como no pudo obtener una copia de la enciclopedia, se preguntó por el tamaño de los volúmenes. Hay unas $4.03 \times 10^{26}$ permutaciones en el texto, número que no solo es mayor que la deuda de EEUU, sino que excede estimaciones sobre el número de granos de arena en la Tierra (menos de $10^{24}$, según
http://www.newton.dep.anl.gov/askasci/ast99/ast99215.htm, pero la página web no menciona quién los contó). Cairoli estima que un millón de monjes fanáticos, escribiendo cada uno una permutación por segundo, hubieran tardado dos mil millones de años en completar la tarea.