|
Solución del problema de Noviembre, 2010
| El problema: |
 |
"Calcule
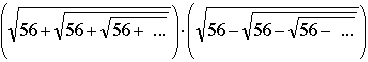
y justifique su respuesta".
|
Respuestas correctas: |
 |
Todos nuestros lectores encontraron una manera de obtener la respuesta correcta, pero aquellos con más experiencia en sucesiones notaron que había una sutileza que tener en cuenta. Hemos separado la lista de respuestas recibidas en dos partes, aquellas que son soluciones completas y aquellas que solamente contienen la respuesta.
Recibimos soluciones completas de
Bojan Bašić
(Serbia) |
Verena Haider
(Austria) |
Matthew Lim
(USA) |
José Borges
(Portugal) |
Benoît Humbert
(Francia) |
Alex Love
(Ontario) |
Shai Covo
(Israel) |
Kipp Johnson
(USA) |
Christian Pont
(Francia) |
Mei-Hui Fang
(Austria) |
Wolfgang Kais
(Alemania) |
John T. Robinson
(USA) |
Philippe Fondanaiche
(Francia) |
Normand Laliberté
(Ontario) |
Albert Stadler
(Suiza) |
Bruce Golfman
(Austria) |
Marc Lichtenberg
(Francia) |
Damian Straszak
(Polonia) |
Correct answers to our November problem were submitted by
Mehdi Abdeh-Kolahchi
(Canada) |
Cornel Gruian
(Rumania) |
Milan Pavic
(Serbia) |
Christopher Abdnour
(USA) |
Tom Holens
(Manitoba) |
Anónimo |
Luigi Bernardini
(Italia) |
Ile Ilijevski
(Macedonia) |
Raffaele Rainone
(Italia) |
Daniel Bitin
|
Hasan Kolcu
(Reino Unido) |
Shpetim Rexhepi
(Macedonia) |
K.A. Chandrashekara
(India) |
Karim Laaouini
(Marocco) |
Francisco Suñol Esquirol
(España) |
Bernard Collignon
(Francia) |
Antonio Ledesma Lopez
(España) |
Mohammad Ali Syed
|
Allen Druze
(USA) |
Farid Lian
(Colombia) |
A. Teitelman
(Israel) |
Sébastien Dumortier
(Francia) |
Pavan Manjunath
(India) |
Paul Voyer
(Francia) |
Amit Elazari
|
Remo Mantovanelli
(Italia) |
Lasse Wollatz
(Alemania) |
Sergey Gleizer
(USA) |
|
|
En primer lugar mostraremos cómo obtener la respuesta, luego discutiremos la sutileza, y finalmente discutiremos algunos asuntos pendientes.
|
La solución:
Respuesta. Sea  . Como x está definido por medio de infinitas raíces, no es obvio que represente un número real; sin embargo, si existe, debe ser positivo (porque la raiz representa la raiz positiva) y debe satisfacer . Como x está definido por medio de infinitas raíces, no es obvio que represente un número real; sin embargo, si existe, debe ser positivo (porque la raiz representa la raiz positiva) y debe satisfacer

Es decir, 0 = x2 - x - 56 = (x - 8)*(x + 7), De manera que x debe ser igual a 8. Similarmente, si y = 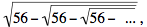
y se cumple que y representa a un número real, entonces debe ser

de manera que 0 = y2 + y - 56 = (y - 7)(y + 8), de done y = 7. Combinando los dos resultados,
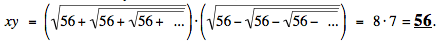
La sutileza. Uno debe proceder con cautela al tratar con infinitos. Tanto x como y fueron definidos utilizando una sucesión infinita de raíces. Estas raíces se llaman "raíces anidadas" (nested radicals) en las páginas de Wikipedia y de MathWorld, donde se puede obtener más información. Hay situaciones en que las raíces anidadas aparecen naturalmente: por ejemplo, la fórmula del medio-ángulo 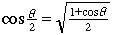 lleva a la sucesión de números lleva a la sucesión de números
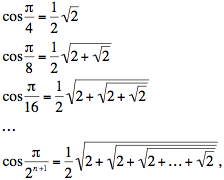
donde en la última expresión hay n números 2. Es probable que la primer aparición de radicales infinitos sea en la notable fórmula de Viète 1593) para 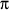 : :
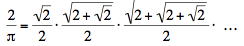 . .
Nuestro x se define como el límite de la sucesión
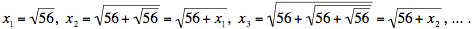 . En general, . En general,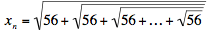 con el número 56 apareciendo n veces, de manera que con el número 56 apareciendo n veces, de manera que
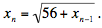
De modo similar, y es el límite de la sucesión definida por
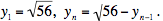
No es para nada obvio que los objetos definidos por medio de sucesiones infinitas deban comportarse como números reales y obedecer las leyes usuales de la aritmética. Como un ejemplo de lo que puede fallar, consideremos la suma infinita
S = 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 + ... .
Si S representa un número real, deberíamos tener
S = 1 – ( 1 – 1 + 1 – 1 + 1 – 1 + 1 –...) = 1 – S,
de donde 2S = 1, y S = ½. Pero se puede decir que
S = (1 – 1) + (1 – 1) + (1 – 1) + (1 – 1) + ... = 0 + 0 + ... = 0.
Y, con igual facilidad,
S = 1 – (1 – 1) – (1 – 1) – (1 – 1) – ... = 1 – 0 – 0 – ... = 1.
¿Qué está pasando? La forma de darle sentido a una suma infinita es definiendo la suma infinita como el límite de una sucesión de sumas finitas,
S1 = 1, S2 = 1 - 1 = 0, S3 = 1 - 1 + 1 = 1, S4 = 1 - 1 + 1 - 1 = 0,... .
En este ejemplo la sucesión alterna entre 0 y 1, y nunca se aproxima a un único número real (que llamaríamos su límite). Tales sucesiones, que no tienen límite, se llaman divergentes y deben ser consideradas de menera diferente que las sucesiones convergentes. Para una sucesión convergente, es decir una sucesión tal que eventualmente se mantiene “arbitrariamente cerca” a un único número real, las reglas usuales de la aritmética se aplican sin problema. Volviendo a nuestro problema de noviembre, debemos probar que ambas sucesiones convergen, xn a 8, e yn a 7. Recibimos varios tipos de demostración, de las que hemos elegido tres.
Demostraciones de la convergencia.
Prueba 1. En base a las demostraciones de Borges y Kais.
Ya sabemos que si la sucesión de radicales anidados
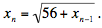 converge, debe ser a 8; alcanza entonces con probar que la sucesión converge, debe ser a 8; alcanza entonces con probar que la sucesión
{8 – xn} tiende a cero:
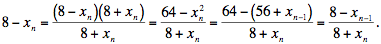
Tomando valor absoluto en ambos lados (y usando que 8 + xn es siempre positivo),
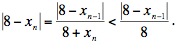
Si repetimos la estimación ahora para n – 1 en vez de n, luego con n – 2, y continuamos hasta |8 - x1| = |8 - √56| , tenemos
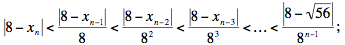
el término de la derecha se aproxima a cero cuando n es grande, lo que prueba que xn está arbitrariamente cerca de 8 cuando n tiende a infinito.
Un argumento análogo muestra que 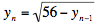 converge a 7: converge a 7:
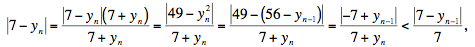
de donde
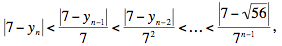
que también tiende a cero cuando n tiende a infinito. Prueba concluida.
Haider y Bašić utilizaron una variante del argumento anterior, donde probaron por inducción que
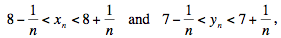
y estas desigualdades implican que {xn}, {yn} convergen a los límites adecuados cuando n tiende a infinito.
Prueba 2. Un resumen de pruebas similares de Covo, Fang, Johnson, Humbert.
Un sencillo argumento por inducción prueba que, para todo n, xn < 8 y además xn+1 > xn. Luego {xn} es una sucesión creciente y acotada por arriba (por 8), lo que implica que tiene límite. Luego uno prueba que el límite es 8. La sucesión {yn} es algo más complicada, porque yn > 7 cuando n es impar, mientras que yn < 7 cuando n es par. Entonces debe mostrarse que los términos impares decrecen al mismo límite a l que crecen los pares. La demostración de esta última aseveración es sencilla.
Prueba 3. Basada en demostraciones que usan cálculo, de Golfman, Pont, Stadler, Straszak.
Consideremos las dos funciones
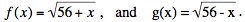
El método iterativo en análisis numérico sirve para resolver ecuaciones de la forma f(x) = x de manera sencilla: si en un entorno de la solución la función tiene derivada cuyo valor absoluto es menor que 1, y se toma x0 dentro de ese entorno, la sucesión {xn} definida por xn = f(xn–1) va a converger a esa solución. Las dos sucesiones de nuestro problea pueden obtenerse poniendo x0 = 0 en la ecuación f(x) = x, e y0 = 0 en la ecuación g(x) =x:
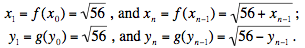
Todo lo que hay que hacer es investigar las derivadas:
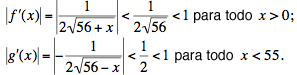
Luego ambas funciones satisfacen las condiciones, lo que nos asegura que ambas sucesiones convergen.
Comentarios. Muchos lectores notaron que 56 puede ser remplazado por cualquier número r >1:
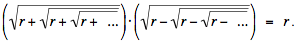
Más aún, un reciente artículo de Javier Peralta ["On Some Infinite Sums of Iterated Radicals", International Journal of Mathematical Education in Science and Technology, 40:2 (March 2009) 290-300] dice probar (pero parecería que falta un paso clave) que, para r > 1,
 es un entero si y solo si r = k(k – 1), es un entero si y solo si r = k(k – 1),
while
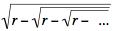 es un entero si y solo si r = k(k + 1). es un entero si y solo si r = k(k + 1).
Cualquiera de los métodos que hemos discutido llevan a una demostración de la afirmación de Peralta.
|