|
Solución del problema de Septiembre, 2010
| El problema: |
 |
Un fontanero cuenta con una pila de tubos rectos de igual longitud, y una caja llena de codos en ángulo recto. El fontanero se da cuenta de que no puede utilizarlos para armar un pentágono, aunque sí puede hacer un polígonos cerrados de 6 y de 7 lados. Pruebe que las observaciones del fontanero son correctas (para aquellos matemáticos sin experiencia en plomería, les aclaramos que los tubos rectos no pueden ser unidos sino mediante un codo, es decir que todos los tubos se unen en ángulo recto).
|
Respuestas correctas: |
 |
Recibimos soluciones de
Bojan Basic (Serbia) |
Verena Haider (Austria) |
Bernard Collignon (Francia) |
Benoît Humbert (Francia) |
Shai Covo (Israel) |
Matthew Lim (USA) |
Mei-Hui Fang (Austria) |
Patrick J. LoPresti (USA) |
Philippe Fondanaiche (Francia) |
John T. Robinson (USA) |
Bruce Golfman (Austria) |
Albert Stadler (Suiza) |
Cornel Gruian (Rumania) |
|
|
La solución:
El pentágono.
Veamos primero la imposibilidad de construir en tres dimensiones un pentágono con cinco ángulos rectos. Fang nos comenta que el resultado se sigue de un teorema de B.L. van der Waerden, en 1970: cualquier pentágono en tres dimensiones que es equilátero y equiangular yace en un plano. El argumento de Van der Waerden [Ein Satz über räumliche Fünfecke. Elem. Math. 25 (1970), 73-78; addendum: Elem. Math 27 (1972), 63] es bastante complicado y hay versiones más simples. (Es muy sencillo obtener una prueba si uno sabe que una isometría en tres dimensiones es o una rotación o el producto de una rotación y a lo sumo dos reflexiones, una en un plano perpendicular al eje de rotación y la otra en un plano que contiene el eje. Ver, por ejemplo, Introduction to Geometry de H.S.M. Coxeter, Secciones 7.1-7.4.) Incluimos abajo dos demostraciones que resultan del enfoque directo tomado por todos nuestros lectores salvo cuatro.
Prueba 1. Tres vértices consecutivos del pentágono ABCDE forman un triángulo isósceles rectángulo con lados 1, 1, √2. Introduzcamos coordenadas con A, B, C en el plano xy: A = (0, 1, 0), B = (0, 0, 0), C = (1, 0, 0). Como CD ⊥ BC, D tiene que estar en el plano x = 1; como D es equidistante de A y B, tiene que estar en el plano y = ½. Además, si llamamos D' al pie de la perpendicular de D al plano xy, entonces CD'D
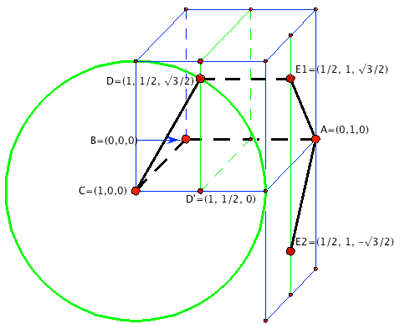
es un triángulo rectángulo 30-60 de lados 1, 1/2, √3/2.
Podemos tomar a D por encima del plano xy, de manera que
D = (1, 1/2, √3/2).
Un razonamiento similar (intercambiando los roles de x, y) nos da dos posibilidades para E:
E1 = (1/2, 1,
√3/2) ó E2 = (1/2, 1,
-√3/2).
En el primer caso, la distancia de D a E es 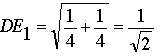 ; en el segundo, ; en el segundo, 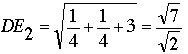 . En cualquier caso, la distancia de D a E no es 1. . En cualquier caso, la distancia de D a E no es 1.
Prueba 2. Robinson mostró más con su argumento: Un pentágono equilátero ABCDE en el espacio 3-dimensional con lados de longitud 1 y ángulos rectos en A, B, C, D debe tener un el ángulo en E de 60° ó cos-1(-5/√14) (que es alrededor de 111°); en particular, ∠E no puede ser 90°. Modificaremos la notación de Robinson para hacerla coincidir con el párrafo anterior. Entonces, las coordenadas de E aún son (1/2, 1, √3/2), pero como hay un ángulo desconocido en E, ya no disponemos de la longitud de DA; solamente sabemos que D está en el plano x = 1, y que DC = 1, de manera que D = (1, cos δ, sin δ) for some angle δ. para un ángulo δ. Para encontrar cos δ usamos ED = 1 para obtener
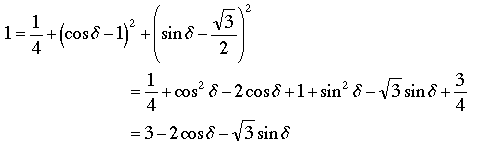
que se simplifica a
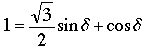 . (1) . (1)
Queremos resolver (1) para cos δ: Sea c = cos δ y remplacemos sin δ por 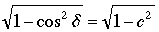 ; ;
entonces (1) se convierte en
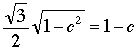 , ,
de manera que elevando al cuadrado,
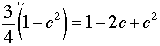 . .
Resolviendo esta cuadrática para c obtenemos
c = cos δ = 1 ó 1/7. (2)
Finalmente, el coseno del ángulo que buscamos es el producto escalar de dos vectores unidad,
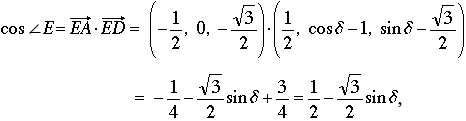
que por (1), es igual a cos d – ½; ahora la ecuación (2) nos dice que cos ∠E = 1– ½ = ½, ó cos ∠E = 1/7 - 1/2 = -5/14, como se quería demostrar.
Comentarios. LoPresti sugiere que llamemos a un plomero cuatri-dimensional, ya que en cuatro dimensiones es trivial construir un pentágono con lados unidad y cinco ángulos rectos. Una forma de ver esto es ponerlo en el subespacio 4-dimensional u + v + x + y + z = √2 del espacio 5-dimensional. Entonces se verifica fácilmente que el pentágono de vértices
(1/√2, 1/√2, 0, 0, 0), (0, 1/√2, 1/√2, 0, 0), (0, 0, 1/√2, 1/√2, 0),
(0, 0, 0, 1/√2, 1/√2), (1/√2, 0, 0, 0, 1/√2),
tiene lados de longitud 1 y diagonales de longitud √2 (lo que implica que los ángulos entre lados consecutivos son rectos). LoPresti no nos dice cuánto cobran los plomeros cuatri-dimensionales; tenemos que el costo podría ser cosa de otro mundo.
La solución de Haider fue completamente diferente. Consistió en considerar los cinco vectores que unen cada vértice del pentágono con el siguente, y determinar que cuatro cualquier de ellos deben ser linealmente independientes; en consecuencia, el espacio más pequeño en que el pentágono puede existir debe tener al menos dimensión cuatro.
Hexágonos, heptágonos, y otros n-gonos con n > 5.
Dicen que ver es creer:
Un hexágono rectángulo Un heptágono rectángulo
Por otra parte, dicen los matemáticos que no debe creerse todo lo que se ve:

Triángulo de Penrose en un parque en Gotschuchen, Austria
Foto obtenida en Wikipedia.
Como los ángulos de un triángulo suman 180°, ningún triángulo puede tener más de un ángulo rector. La ilusión de un triángulo con tres ángulos rectos fue concebida, según Wikipedia, en 1934 por el artista suizo Oscar Reutersvärd; fue descubierta independientemente por el matemático británico Roger Penrose y su padre Lionel Penrose, el conocido psiquiatra y geneticista británico.
Es sencillo probar la existencia de un hexágono rectángulo sin utilizar coordenadas: consideremos los lados que rodean la región formada por dos caras adyacentes en un cubo (como en la imagen con los tubos arriba, y como en el diagrama de abajo a la izquierda). Lim y Golfman describieron un segundo ejemplo usando los lados de un cubo: tomando lados a lo largo de un camino en el que dos lados consecutivos pertenecen a la misma cara, pero nunca tres (dibujo de abajo a la derecha).
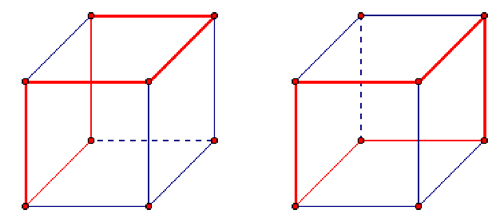
Los caminos considerados en las figuras son:
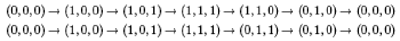
Para el heptágono, puede ayudar imaginarse la figura apoyada sobre una escalera. La porción del escalón de abajo consiste en tres lados de un cuadrado. La parte vertical central consiste de dos lados de un trapezoide isósceles ABCD con AB = BC = CD = 1, y AD || BC con AD = √2. Como se ve en la figura, se puede pensar en el triángulo isósceles rectángulo ADP como una aleta que hace bisagra sobre el lado AD.
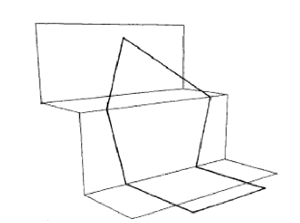
Cuando la aleta está "abierta" (con P fuera del trapezoide, pero en el mismo plano
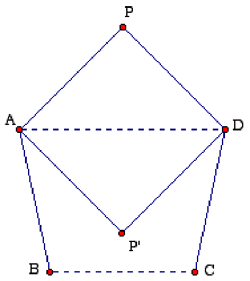
vertical), ∠BAP > ∠P'AP = 90°; con la aleta "cerrada" (en la posición AP'D), ∠BAP' < ∠BAD < 90°. En algún lugar entre ambas posiciones, ∠BAP = ∠CDP = 90°. También habrá una posición simétrica con la aleta del otro lado del plano vertical donde el ángulo entre lados adyacentes será 90°. Aunque la mitad de los lectores usaron un argumento dinámico similar, todos proporcionaron coordenadas. He aquí las coordenadas que suben los escalones (con las direcciones positivas de x,y,z hacia la derecha, adentro, y arriba respectivamente):
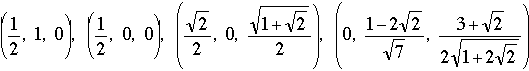
Los tres vértices a la izquierda en la figura de la escalera tienen coordenadas negativas en x, pero los mismos valores para y,z. Se verifica fácilmente que la distancia entre vértices consecutivos es 1, y que el ángulo entre lados consecutivos en 90°.
Comentarios finales.
Como señalaron varias respuestas, existen n-gonos equiláteros rectángulos para n = 4, y para todo n ≥ 6 — solamente fallan 3 y 5. Para un k-gono que termina en los tres lados de un cuadrado (como por ejemplo el hexágono de la izquierda en la figura de los cubos y el heptágono en la escalera), construimos un (k+2)-gono remplazando
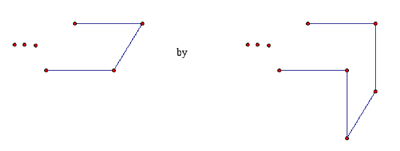
k-gon (k+2)-gon
La figura con el heptágono en la escalera viene de la solución del problema 1110 (propuesto por Gerald Wildenberg) en Mathematics Magazine, 55 (1982) 47-48, que fue la fuente del problema de este mes.
|