El rompecabezas no puede resolverse luego del cambio de piezas. Hubo cierto desacuerdo respecto a cuánto le llevaría a Sophie y Sally darse cuenta, pero la mayoría opinó que abandonaron luego de un tiempo finito.
Nuestro problema de febrero está adaptado de un problema del capítulo 2 ("Coloring Proofs") en Problem Solving Strategies de Arthur Engel, (Problem Books in Mathematics. Springer-Verlag, New York, 1998.) Agradecemos a Matthieu Dufour por presentarnos el problema. De alguna manera hemos omitido decir que Sophie y Sally no son realmente dos niñas, sino los gatos del vecino.
Además, hemos (tal vez poco sabiamente) formulado el problema sugiriendo que hasta un gato podría completar el rompecabezas luego del cambio de piezas. Pedimos perdón a todos aquellos que pasaron una tarde en cálculos inútiles. Efectivamente, si se colorea el tablero de 10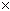 
10 como en la figura,
es fácil convencerse de que el rompecabezas puede ser completado solamente si hay un número impar de piezas de 2 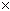2: cada pieza de 2 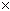2 cubre exactamente un cuadrado rojo, mientras que cada pieza de 1 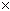4 cubrirá 0 ó 2 cuadrados rojos; como hacen falta 25 piezas para cubrir el tablero, tiene que haber un número impar de aquellas que cubren un cuadrado rojo. Como sabemos que el rompecabezas fue completado tanto por Sophie como por Sally, sabemos que el número total de piezas de 2 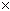2 era impar. Luego del intercambio, cada una tiene un número par de piezas de 2 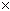2, de manera que ya no es posible completar ninguno de los rompecabezas.
Amghibech y Cairoli nos enviaron la solución presentada arriba. Hemos recibido también otras astutas soluciones. He aquí dos más. Y otras pueden ser vistas en nuestra página en francés.
Coloreando el tablero a la manera de Billion.
Tomemos el rompecabezas completado y coloreemos las columnas verticales alternativamente en blanco y rojo. Quitemos las piezas de 2 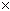2 y aquellas de 1 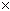4 puestas horizontalmente. Estas piezas tendrán un mismo número de cuadrados de cada color, de manera que las piezas restantes también tendrán un mismo número de cuadrados de cada color. Pero las piezas de 1 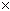4 que quedan tendrán todos sus cuadrados en rojo, o todos en blanco, lo que implica que el número de piezas de 1 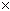4 colocadas verticalmente es par. Del mismo modo vemos que el número de piezas de 1 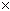4 colocadas horizontalmente debe ser par. Concluimos que el rompecabezas completado debe tener un número par de piezas de 1 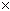4; luego, no puede completarse el rompecabezas usando una piezas más de 1 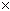4 tile, ni usando una menos.
Argumento combinatorio. Un ejemplo de este tipo de solución es la de Tifenbach:
Supongamos el rompecabezas resuelto con el número adecuado de piezas de 1 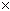4 y 2 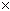2. Sea s(j) el número de cuadrados en la fila j (empezando de arriba) cubierto por 1 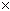4's verticales. Cada s(j) es par, ya que los 1 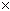4 horizontales y los 2 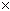2 cubren 4 y 2 cuadrados, respectivamente, de cada fila, y esa fila tiene 10 cuadrados. Sea t(j) el número de 1 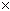4 verticales cuyo tope está en la fila j. t(1) = s(1), y entonces t(1) es par. Además, por recursión vemos que cada t(j) es par:
