|
|
|
Centro matemático - Centromatemático.com |
 |
 |
Problemas de 2006-2007
|
 |
 |
 |
 |
| PM69: mayo, 2007 |
 |
¿Hallar todos los enteros positivos n que satisfacen
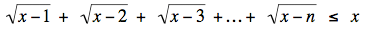
para todo número real x ≥ n?
|
 Solución. Solución.
|
| PM68: abril, 2007 |
 |
Decimos que dos puntos sobre una esfera son ortogonales si las rectas que unen dichos puntos al centro de la esfera son perpendiculares. Por ejemplo, el polo norte es ortogonal a cualquier punto del ecuador, y no es ortogonal a ningún otro punto. Cuál es el mínimo número de colores necesarios para colorear la esfera de manera que ningún par de puntos ortogonales tenga el mismo color?
|
 Solución. Solución.
|
| PM67: marzo, 2007 |
 |
Probar que hay infinitos enteros tales que
(i) el número es divisible por la suma de sus dígitos
(ii) ninguno de sus dígitos es cero.
|
 Solución. Solución.
|
| PM66: febrero, 2007 |
 |
Sophie y Sally recibieron un rompecabezas cada una para Navidad. El de Sophie era una grilla de 10 por 10 que debe ser llenada por un cierto número de piezas de 1 por 4, y cierto número de piezas de 2 por 2, usando todas las piezas. El de Sally también era una grilla de 10 por 10 que debía ser llenada por un cierto número de piezas de 1 por 4, y por cierto número de piezas de 2 por 2, usando todas las piezas. Sophie pudo terminar el suyo en 2 minutos y medio, y Sally el suyo en 4 minutos. Luego intercambiaron los rompecabezas, y Sophie hizo el de Sally en en 4 minutos y 20 segundos, mientras que Sally completó el de Sophie en 3 minutos y 12 segundos. Luego volvieron a sus rompecabezas originales, pero Sophie le dio a Sally una de sus piezas de 1 por 4, y Sally a Sophie una de sus piezas de 2 por 2. Nuestro problema: ¿cuánto le llevó a cada una terminar su rompecabezas esta vez?
|
 Solución. Solución.
|
| PM65: enero, 2007 |
 |
El número 5·734 tiene muchos dígitos en su representación decimal. Sin evaluar, probar que un dígito ocurre al menos cuatro veces en el número.
|
 Solución. Solución.
|
| PM64: diciembre, 2006 |
 |
Para la temporada de fiestas ofrecemos un truco matemático para asombrar a amigos y parientes. No se requiere entrenamiento especial, solamente una mesa y 45 monedas.

Ponga las 45 monedas en la mesa y pida a un voluntario que le vende los ojos a usted (este paso es opcional) y que después ordene las monedas en tantas pilas como quiera. Él podría, por ejemplo, hacer una pila de 24 monedas, una de 20, y otra de 1. Pídale que quite una moneda de cada una de sus pilas y que haga una nueva pila (en nuestro ejemplo la pila nueva tendría 3 monedas y quedarían dos pilas más de 23 y 19). Indique repetir el proceso - esto es, quitar una moneda de cada pila (incluyendo la nueva) para formar una pila nueva (lo que nos dejaría en el ejemplo con pilas de 22, 18, 3, y 2), y luego continuar repitiendo el proceso. Después de un lapso de tiempo adecuado, dependiendo de la configuración inicial y la habilidad del voluntario, usted anuncia que hay una pila de cada tamaño de 1 a 9.
Nuestro problema para diciembre: probar que el truco siempre funciona.
No conocemos el origen de este problema. Lo aprendimos de Igor Astapov, profesor del Royal Military College of Canada, quien a su vez lo aprendió en una página rusa de chat matemático.
|
 Solución. Solución.
|
| PM63: noviembre, 2006 |
 |
Comenzamos con dos números reales positivos a0 y a1, y formamos una sucesión infinita cuyos términos satisfacen
an+1 an-1 = an + 1.
Demuestre que an+5 = an para todo n.
|
 Solución. Solución.
|
| PM62: octubre, 2006 |
 |
La tarea es convertir
x2 + 10 x + 20 en x2 + 20 x + 10
en 50 pasos o menos, donde en cada paso está permitido
sumar o restar 1 sea al coeficiente constante o al de x (pero no a ambos).
Además, cada paso debe producir un polinomio que
no pueda factorizarse como (x+m)(x+n) con m,n enteros;
por ejemplo, en el primer paso no se puede reducir el 10 a 9 porque x2+9x+20=(x+5)(x+4) .
|
 Solución. Solución.
|
| PM61: septiembre, 2006 |
 |
- Alrededor de una mesa circular hay 15 sillas equidistantes, cada una frente al cartel con el nombre de uno de los 15 delegados. Al sentarse, los delegados no se dan cuenta de que sus nombres están escritos en los carteles y, sorprendentemente, ningún delegado queda sentado frente a su cartel. Pruebe que se puede rotar la mesa de manera que al menos dos delegados quedan frente a sus respectivos carteles.
- Dé un ejemplo de arreglo en el que solamente uno de los delegados está sentado frente a su cartel, y tal que ninguna rotación sitúa correctamente más de uno.
|
 Solución. Solución.
|
|
|
 |