|
|
|
Centro matemático - Centromatemático.com |
 |
 |
Problemas de 2005-2006
|
 |
 |
 |
 |
| PM60: mayo, 2006 |
 |
Encuentre el máximo común divisor de los 1003 enteros
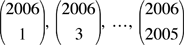
|
 Solución. Solución.
|
| PM59: abril, 2006 |
 |
Dos jugadores toman turnos eligiendo un coeficiente ai del polinomio
x10 + a9 x9 + ... + a1 x + 1
y remplazándolo con un número real cualquiera. El juego termina luego de 9 movidas, cuando todos los ai han sido elegidos. El primer jugador gana si el polinomio resultante no tiene raíces reales, mientras que el segundo gana si el polinomio tiene al menos una raiz real. Existe una estrategia ganadora para uno de los jugadores: gana no importa lo que haga el rival. Qué jugador es, y cuál es la estrategia ganadora?
|
 Solución. Solución.
|
| PM58: marzo, 2006 |
 |
Juan escribe un número con 2187 dígitos en el pizarrón, cada dígito un 1 o un 2. Judith crea un nuevo número, a partir del de Juan, leyendo de izquierda a derecha y reemplazando cada 1 por 112 y cada 2 por 111 (por ejemplo, si el número de Juan empieza con 2112, el de Judith empieza con 111112112111).
Cuando Judith termina de escribir su número, nota que los primeros 2187 dígitos empezando de la izquierda en su número y el de Juan son los mismos. Cuántas veces ocurren 5 unos consecutivos en el número de Juan?
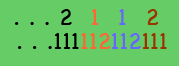
|
 Solución. Solución.
|
| PM57: febrero, 2006 |
 |
Dado un par de ecuaciones cuadráticas a coeficientes enteros b y c, x2 - bx + c = 0 y x2 - bx - c = 0, decimos que son compatibles si ambas tienen soluciones enteras.
Por ejemplo,
x2 - 5x + 6 = 0 tiene soluciones 2 y 3, mientras que
x2 - 5x - 6 = 0 tiene soluciones -1 y 6.
Por supuesto, podemos multiplicar b y c por d y d2 para obtener el par relacionado x2 - bdx ± cd2 = 0, pero estamos interesados en pares donde b y c no tienen divisores comunes. Hay algún otro par compatible?
El problema de este mes está basado en el artículo "Curious Consequences of a Miscopied Quadratic",por Jeffrey L. Poet y Donald L. Vestal, Jr. en el College Mathematics Journal, 36:4 (September 2005), pp 273-277.
|
 Solución. Solución.
|
| PM56: enero, 2006 |
 |
Feliz Año Nuevo! El equipo del Problema del mes te desea tanta salud y felicidad este año como las que disfrutaste el año pasado:
Encuentra el máximo valor posible de f(2006) - f(2005) donde f es una función a valores reales que satisface la desigualdad
|f(x) - f(y)| ≤ (x-y)2
para todo par de números reales x e y.
|
 Solución. Solución.
|
| PM55: diciembre, 2005 |
 |
Las manecillas de mi reloj se mueven de modo continuo. En el preciso instante en que el segundero pasa por una de las doce subdivisiones de la esfera, sé que en menos de medio segundo el minutero va a pasar justamente sobre el horario (la manecilla que indica la hora). A qué hora ocurre ésto, si es antes del mediodía?
|
 Solución. Solución.
|
| PM54: noviembre, 2005 |
 |
El profesor Adams escribió en el pizarrón un polinomio f(x), a coeficientes enteros, y dijo: "hoy es el cumpleaños de mi hijo, y si evaluamos el polinomio en su edad A, tenemos f(A)=A. Notarán también que f(0)=p, y que p es un número primo mayor que A". ¿Qué edad tiene el hijo del profesor Adams?
|
 Solución. Solución.
|
| PM53: octubre, 2005 |
 |
El primer jugador lanza una moneda 1001 veces, mientras que el segundo jugador lo hace solamente 1000 veces. Cuál es la probabilidad de que el primer jugador obtenga más caras? (Por favor, evita los cálculos engorrosos.)
|
 Solución. Solución.
|
| PM52: septiembre, 2005 |
 |
Nuestro primer problema en esta nueva temporada trata con enteros. Como ejercicio luego de las largas vacaciones veraniegas, puedes intentar probar que para cualquier número impar n, 4n + 1 es múltiplo de 5. Para el problema de septiembre debes
Probar que si el número n es impar y mayor que 3, entonces 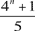 no puede ser primo. no puede ser primo.
|
 Solución. Solución.
|
|
|
 |