|
Solución del problema de mayo, 2007
| El problema: |
 |
¿Hallar todos los enteros positivos n que satisfacen
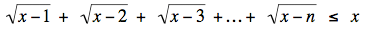
para todo número real x ≥ n?
|
Respuestas correctas: |
 |
Martin Argerami (Regina) |
Normand LaLiberté (Ontario) |
Christophe Brighi (Francia) |
Matthew Lim (USA) |
Qin Deng (Toronto) |
John T. Robinson (USA) |
Sébastien Dumortier (Francia) |
K. Sengupta (India) |
Stefan Gatachiu (Rumania) |
Bob Franz (USA) |
| Wolfgang Kais (Alemania) |
Xavier Hecquet (Francia) |
|
La solución:
Solución. Sólo n = 1 y n = 2 satisfacen la desigualdad dada.
En efecto, para n = 1 tenemos x – 1 < x, de manera que para x ≥ 1
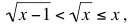
como se pedía.
Para n = 2 y x ≥ 2, comencemos con (x – 2)2 ≥ 0, que implica x2≥ 4x – 4. Tomando raiz cuadrada en ambos lados,
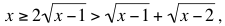
como se pedía.
Para n ≥ 3, la desigualdad falla para valores adecuados de x. De hecho siempre falla para x = n + 1. Probamos esto basado en dos simples desigualdades:
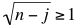 para j yendo de 0 a n – 1, y para j yendo de 0 a n – 1, y-
Prueba de que 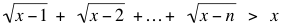 cuando x = n + 1: cuando x = n + 1:
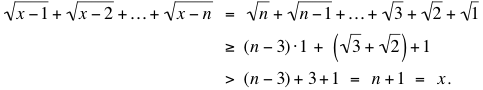
Comentarios.
Además de resolver nuestro problema, John Robinson investigó el comportamiento de la diferencia entre x y la suma de las raíces cuadradas
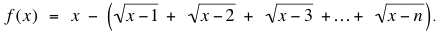
Como vimos antes, la function es negative si n ≥ 3 y x = n+1; además, es claro que para x > n2 es positiva. Robinson pudo mostrar que f(x) cambia de negative a positive cerca de n2– n/2. Más precisamente, cuando n < 4, y además x es un entero,
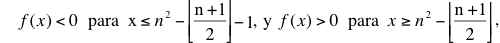
donde los corchetes inferiores indican la parte entera. Entonces, por ejemplo, con n = 5 y
x = 52 – (5 + 1)/2 obtenemos
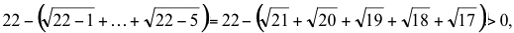
mientras que
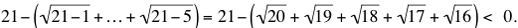
Probó esto cambiando cada raíz cuadrada por su polinomio de Taylor de grado dos
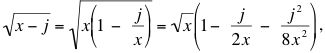
y sumando.
Matthew Lim se preguntó qué clase de resultado se obtiene en nuestro problema cuando las raíces cuadradas son reemplazadas por raíces k-ésimas. Pudo probar (por inducción) que para n ≥ 2k – 1 y x = n + 1 tenemos
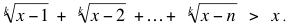
No pudo, sin embargo, decir cómo se compara la suma con x cuando n < 2k – 1, salvo en el caso de nuestro problema (donde k = 2).
|