De manera que z = u, de donde an+5 = an para cualquier n, como se buscaba.  Como todos los términos son positivos, no tenemos que preocuparnos por dividir por cero, de manera que todos los pasos son válidos. Como señala Mir, podemos relajar la condición de positividad pidiendo simplemente a₀ + 1 ≠ 0 , a₁ + 1 ≠ 0, y a₀ + a₁ + 1 ≠ 0.

Un atajo debido a Saïd Amghibech (que hemos modificado un poco).
Usamos la misma notación que en la primera solución. Multiplicando (4) por w, tenemos

wxz =₍₄₎ wy + w =₍₃₎ x + 1 + w =₍₂₎ x + xv = x(1 + v) =₍₁₎ xuw

Cancelando wx en ambos lados concluimos que z = u.

            Podemos encontrar otra solución sencilla si notamos que la condición dada es simétrica en n+1 y n-1; en otras palabras, la formula para n creciente es la misma que para n decreciente. Esto sugiere comenzar en el medio, poniendo a_n = w, a_n+1 = x. 

Tenemos

,

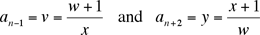de donde deducimos (como en la primera solución)

.

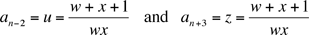De este modo conseguimos ver que a_n-2 = a_n+3 para todo n, lo que es otra manera de decir que la sucesión es un 5-ciclo.

Una solución de Gauss.
Para ser honestos, Gauss no nos envió ninguna solución. La obtuvimos de H.S.M. Coxeter en su artículo "Frieze Patterns", Acta Arithmetica 26 (1971), 297-310.  Ver las páginas 297 y 298.  En palabras de Coxeter,
         La historia comienza en 1602, cuando Nathaniel Torporley (1564-1632) comenzó a investigar las cinco “partes” a, A, b, B, c de un triángulo rectángulo esférico (con el ángulo recto en C). Según De Morgan, Torporley anticipó en unos doce años las famosas reglas de Napier que Gauss incluyó en su pentagramma mirificum.  [Las reglas de Napier permiten derivar una gran parte de la trigonometría esférica con muy poco esfuerzo; ver, por ejemplo, el artículo sobre las reglas de Napier en Wikipedia]. Gauss utilizó la identidad

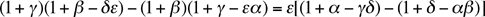
para probar que tres cualesquiera de las cuatro relaciones

implican la restante y que además .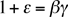 

El pentagramma mirificum es un pentagrama esférico formado por cinco arcos de círculo máximo octogonales.

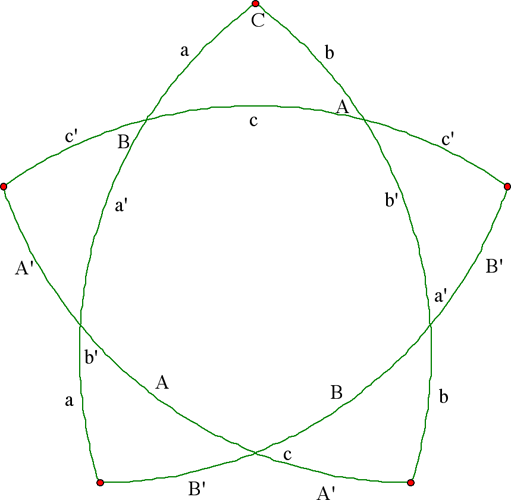
El “núcleo” del pentagrama es un pentágono cuyos vértices son (obviamente) polos de los cinco arcos; decimos entonces que es un pentágono auto-polar. [Esto quiere decir que si un vértice del pentágono interior se pone en el polo norte de la esfera, el lado opuesto queda sobre el ecuador]  La figura completa puede ser derivada del triángulo rectángulo ABC (dibujado en la parte superior) extendiendo los lados y dibujando los arcos de círculo máximo polares de los vértices A y B. Usando x’ para indicar el complemento

x' = ¹/₂ π - x,

vemos fácilmente que los lados del pentágono auto-polar son

A, B, b', c, a',

mientras que los restantes arcos y ángulos son como indica la figura. Claramente, cualquier ecuación que conecte la cinco “partes”, sigue siendo válida cuando se las permute en forma cíclica. Esta es la observación de Napier (salvo que él usó el ciclo alternado a', B, c, A, b'). 

Gauss definió

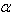    = tan² A,  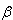                = tan² B,  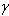          = tan² b',
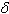      = tan² c,  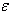                    = tan² a'

y usó una de las relaciones clásicas (como por ejemplo cos c = cot A cot B) para deducir

sec² A = 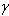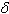,                sec² B =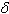 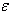,          sec² b' = ,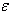   

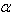sec² c = 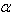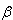,                 sec² a' = .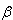

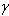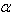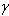
Estas igualdades implican que 1 + = 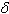, y así con las demás igualdades.  Coxeter agrega mayores explicaciones y aplicaciones. En particular, aplica la sucesión como base para la trigonometría en el plano hiperbólico, pero por ahora interrumpimos la historia aquí.