Solución del problema de abril, 2008

El problema:
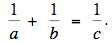
	PM77: Abril 2008 Sean a,b,c enteros positivos coprimos entre sí (es decir, el máximo común divisor es 1) tal que Pruebe que a+b, a-c, y b-c son cuadrados perfectos.

Respuestas correctas:

El problema de este mes viene de Problem of the Week número 1094 (Marzo 27, 2008), de Andrew Beveridge en Macalester College, St. Paul, Minnesota; su fuente fue School Science and Mathematics 63 (Octubre 1963), p. 60.           Recibimos soluciones correctas de Bojan Basic (Serbia) Wolfgang Kais (Alemania) Gérard Billion (Francia) Normand LaLiberté (Ontario) Lou Cairoli (USA) Matthew Lim (USA) John Campbell (Alberta) Richard McIntosh (Regina) Olivier Cyr (Francia) Jacques Mertzeisen (Francia) Dan Dima (Rumania) Giovanni Parzanese (Italia) Philippe Fondanaiche (Francia) Ananda Raidu (India) Mudit Goel (India) John T. Robinson (USA) Xavier Hecquet (Francia) K. Sengupta (India)   A. Teitelman (Israel) También recibimos tres soluciones parciales.

La solución:

Solución. Empezamos multiplicando ambos lados de 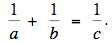 por abc para obtener
                                                             (a + b)c = ab.                                            (1)
Sabemos además que el máximo común divisor de a, b, y c es 1, que escribimos
                                                           mcd(a, b, c) = 1.                                          (2)
Si denotamos los máximo común divisores como

d = mcd(a, b),  e = mcd(a, c), f = mcd(b, c),

la solución del problema pasa por mostrar que a + b = d², a – c = e², b – c = f².  Las respuestas recibidas deducen esto usando una variedad de argumentos; reproducimos aquí los dos métodos más populares. Luego mostraremos un tercer argumento que como subproducto prueba el Ultimo Teorema de Fermat para exponentes negativos.

Método 1.
La ecuación (1) implica que  ac < ab, bc < ab, de manera que  c es menor que a y b, de donde

r := a – c   y  s := b – c

son dos enteros positivos. Remplazamos a = r + c, b = s + c en (1) para obtener (r+c+s+c)c = (r+c)(s+c), que se simplifica a
                                                                  c² = rs.                                                 (3)
Sea k un divisor común de r y s.  Por (3), k divide a c, lo que implica que k también divide a a = r+c y b = s+c, y entonces (por (2)) k=1.  En otras palabras, r y s son coprimos. En consecuencia, (3) implica que r = a – c y s = b – c son cuadrados perfectos, como se pedía (Detalles: por (3) cualquier factor primo de c es también factor primo de exactamente uno de r o s, y recíprocamente; como cualquier primo aparece un número par de veces como factor de c², debe aparecer la misma cantidad de veces como factor de r o de s.)  Resta mostrar que a+b es un cuadrado perfecto. Pero eso se sigue de aplicar (1) a lo que ya sabemos:

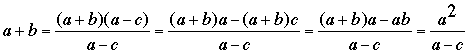
que es un entero escrito como cociente de dos cuadrados, de manera que debe ser un cuadrado como se pedía.

Hemos completado el argumento, pero la demostración nos provee de más información:
Como a – c y b – c son cuadrados perfectos, podemos escribirlos como

r = a – c = u²  y   s = b – c = v²,   u,v > 0, mcd(u, v) = 1.

Se sigue de (3) que c = uv; luego, podemos caracterizar todos los tripletes de enteros a, b, c tales que mcd(a, b, c) = 1 y 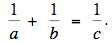Hay una correspondencia biyectiva entre los tripletes (a, b, c) y pares de enteros positivos coprimos u y v tales que

a = u(u + v), b = v(u + v), y c = uv.

Por ejemplo, eligiendo u= 2 y v = 5 tenemos .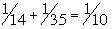

Método 2.
            Recordemos que hemos definido d = mcd(a, b),  e = mcd(a, c), and  f = mcd(b, c).  Notemos primero que cada par de d, e, f es coprimo como consecuencia de (2).  Por ejemplo, mcd(d, e) = 1 porque cualquier divisor de d necesariamente divide a a y b, mientras que cualquier divisor de e necesariamente divide a a y c; en consecuencia, cualquier divisor de d y e divide a a,b,c y es por tanto igual a 1. Cualquier divisor primo de a divide al lado derecho de la ecuación (1), y entonces divide a (a+b), y entonces a b, o divide a c; sin embargo, debido a (2) un divisor primo de   a no puede dividir a b y  cal mismo tiempo. En otras palabras,

Todo divisor primo de a divide a b o c, pero no a ambos.

Esto implica que todo divisor primo de a divide exactamente a uno de d o e, de donde

a = de.

De modo similar obtenemos

b = df   y   c = ef.

Remplazando estos valores de a, b, c en (1) obtenemos (de + df)ef = d²ef, lo que implica

e + f = d.

El resultado buscado se sigue inmediatamente:

a + b = de + df = d(e + f) = d²
a - c = df - ef = e(d - f) = e²
b - c = df - ef = f(d - e) = f²

Método 3 (Richard McIntosh).

Dividiendo xⁿ + yⁿ = zⁿ por (xyz)ⁿ tenemos (yz)^-n + (xz)^-n = (xy)^-n Consideramos soluciones multiples como equivalentes, y escribimos (x,y,z) ∼ (kx,ky,kz), donde
k ε Q -{0}.

Definamos

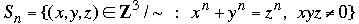
y

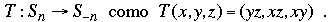
[Comentario: para aquellos lectores que no están acostumbrados a esta elegante notación, la necesitamos solamente por razones técnicas. Puede ser preferable ir directamente al final y ver cómo funciona en un ejemplo. Mientras, simplemente considere tripletes como (3, 4, 5) y (6, 8, 10) el “mismo” triplete pitagórico ya que
3² + 4² = 5² y 6² + 8² = 10², sin múltiplos uno del otro. Note que T lleva (3, 4, 5) a (20, 15, 12), y éste es llevado por T a (180,240,300) = (60·3, 60·4, 60·5) ~ (3, 4, 5).]

Como T(T(x,y,z) = (x²yz, xy²z, xyz²) ~ (x,y,z), se sigue que T es biyectiva. Un argumento directo muestra que si mcd(x,y,z) = 1, entonces mcd(yz, xz, xy) = mcd(x,y)·mcd(x,z)·mcd(y,z).
            Supongamos que n = 1, x + y = z.  Si mcd(x,y,z) = 1, entonces mcd(x,y) = mcd(x,z) = mcd(y,z) = 1, y por el párrafo anterior, mcd(yz, xz, xy) = 1.  Entonces todas las soluciones de 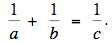 que satisfacen mcd(a, b, c) = 1 son del a forma (a, b, c) = (yz, xz, xy) con x + y = z, mcd(x,y,z) = 1.  En consecuencia,

a + b = yz + xz = (x+y)z = z² = [gcd(a,b)]²,
a – c = yz – xy = (z – x)y = y² = [gcd(a,c)]²,
b – c = xz – xy = (z – y)x = x² = [gcd(b,c)]².

El Método 3 tiene dos simples consecuencias.

1. Tenemos una segunda caracterización de las soluciones — para cada par de enteros positivos coprimos x, y, ponemos z = x + y.  Esto nos da el triplete a = yz, b = xz, c = xy.  Usando el ejemplo del final del Método 1, tomamos x = 2, y = 5, de manera que z = 2 + 5 = 7.  Dividiendo esta suma por 2·5·7 tenemos
   
   
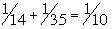
2. El argumento lleva al siguiente interesante resultado:

Corolario. Existen enteros no nulosa, b, c tales que aⁿ + bⁿ = cⁿ si y sólo si n es
1, 2, –1, ó –2.
Proof. La parte difícil de la demostración viene por cortesía de Fermat y Wiles, que eliminaron los casos n ≥ 3.  Nuestro argumento de arriba establece que hay una solución para un entero n si y sólo si la hay para –n.