|
Solución del problema de Deciembre, 2007
| El problema: |
 |
PM73: Deciembre 2007
Para la temporada de vacaciones ofrecemos un truco matemágico con el que podrá asombrar a sus amigos y parientes que reciban una calculadora de regalo:
- Dígales que elijan un número entre 1 y 1000. Llámelo N.
- Luego pídales que calculen 1 más 1/N más dos veces la raiz cuadrada de 1/N; luego tomen la raíz cuadrada del resultado y guárdenla en la memoria presionando el botón M+.
- Ahora pídales que calculen 1 + 1/N menos dos veces la raíz cuadrada de 1/N; luego tomen la raíz cuadrada del resultado y súmenla en la memoria presionando el botón M+.
-
Finalmente, pídales que recuperen el número de la memoria presionando MR (dicho número es la suma de los obtenidos en los pasos 2 y 3). Al mismo tiempo, entrégueles un sobre cerrado que usted sacó de su bolsillo, y pídales que lo abran. Cuando lean el número, pregunte
"es el número que obtuviste, no es cierto?"
Por supuesto, usted tendrá que preparar el sobre con el número por anticipado. La pregunta del mes es,
cuál es el número mágico que debe poner dentro del sobre?
Explique su respuesta.
|
Respuestas correctas: |
 |
Recibimos soluciones correctas de
Theerasak Asawanonwiwat (Tailandia) |
Nouini Kacem (Francia) |
Bojan Basic (Serbia) |
Wolfgang Kais (Alemania) |
Gérard Billion (Francia) |
Normand LaLiberté (Ontario) |
Lou Cairoli (USA) |
Jean-Luc Luyet (Suiza) |
John Campbell (Alberta) |
Jacques Mertzeisen (Francia) |
K.A. Chandrashekara (India) |
Nikhil V. Nair (India) |
Dave Denison (Internet) |
Viktor Pačnik (Eslovenia) |
Sébastien Dumortier (Francia) |
Wilfried Pillard (Francia) |
Philippe Fondanaiche (Francia) |
John T. Robinson (USA) |
Alenka Gabrovec (Eslovenia) |
K. Sengupta (India) |
Xavier Hecquet (Francia) |
Heri Setiyawan (Indonesia) |
Rizwan A. Hussain (Fiji) |
Steve Sparling (British Columbia) |
Yitz Itzik (Internet) |
A. Teitelman (Israel) |
|
La solución:
El número mágico es 2. Nuestros lectores descubrieron el número usando uno de dos métodos similares.
Aunque el análisis no cambia si tomamos a N como un número real mayor o igual que 1, el problema implica claramente que estamos hablando de un entero positivo. Sea s = √(1/N).
Notemos que 0 < s ≤ 1. En ese caso los números almacenados en la calculadora son
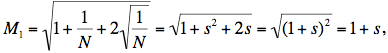
y
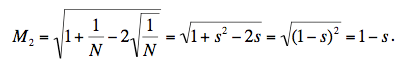
Debemos tener cuidado de asegurarnos de que estamos hablando de la raíz positiva de un número positivo: el primer grupo de igualdades es válido porque s > 0, mientras que el segundo lo es porque s ≤ 1. (Notar que si s > 1, entonces M2 sería s – 1.) El número mágico es entonces
M = M1 + M2 = 1 + s + 1 – s = 2
Lamentablemente hay calculadoras que mostrarán 1.9999999 o 2.0000001 en lugar de 2. Aunque la mayoría de nosotros entendemos sobre errores de redondeo, tales resultados van a disminuir el impacto de nuestro truco. Por supuesto, los magos profesionales tendrán preparada una broma para cuando falle el truco. Tal vez podamos echarle la culpa a la pobre calidad de la mano de obra en un país que no queremos nombrar porque no queremos avergonzarlos poco antes de que organicen las olimpíadas del 2008.
Finalmente, el método alternativo es calcular M2. Aquí es conveniente poner x = 1/N, de manera que
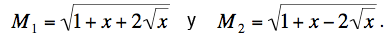
Usando la fórmula
(a + b)(a - b) = a2 - b2
con a = 1 + x y b = 2√x tenemos
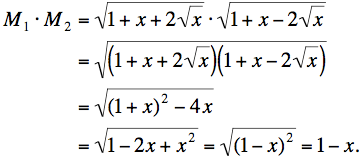
Notemos el detalle en la Segunda línea. Necesitamos usar √p · √q = √(pq), que vale solamente cuando p y q son no-negativos. Las condiciones sobre N—que N ≥ 1—aseguran que x ≤ 1, y entonces p = 1 + x + 2√x > 0 y q = 1 + x - 2√x ≥ 0, haciendo válido el cálculo.
Calculemos M2:
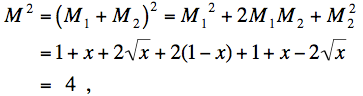
obteniendo nuevamente que M = 2.
|