Solución del problema de febrero, 2008

El problema:

PM75: febrero 2007 Un plano vertical contiene un círculo y un punto P, que está ala izquierda del círculo y por arriba de la línea horizontal sobre la que se apoya el círculo. Su tarea es estirar un cable en línea recta desde P hasta un punto Q en el círculo tal que una cuenta que deslice por el cable llegue al círculo en el mínimo tiempo posible. La única fuerza que actúa sobre la cuenta es la gravedad. El camino más corto es a lo largo de la línea que une P con el centro del círculo, mientras que el camino con mayor pendiente es tangente al círculo. Algún camino intermedio tendrá la combinación exacta de longitud y pendiente , y usted debe determinar cuál es.                Todos recordamos de la escuela que el cable y el aire carecen de fricción; Newton nos ha informado que para un cuerpo que se mueve con aceleración constante la relación entre la distancia s, la velocidad v, y el tiempo t es                         s = 1/2 vt; y si m  es la masa de la cuenta, g es la gravedad, y h es la componente vertical de la línea entre P y Q, entonces la energía potencial mgh de la cuenta en el punto P es igual a  1/2mv2, donde v es la velocidad de la cuenta al llegar a Q.

Respuestas correctas:
	Recibimos soluciones correctas de Gérard Billion (Francia), Philippe Fondanaiche (Francia), Farid Lian Martinez (Colombia), Richard McIntosh (Regina), Jacques Mertzeisen (Francia), Matthew Lim (USA), Giovanni Parzanese (Italia), John T. Robinson (USA).  Las soluciones más cortas redujeron el problema a geometría. Veremos dos de ellas.

La solución:

Método Geométrico 1.  (Billion, Mertzeisen, Parzanese y Robinson).

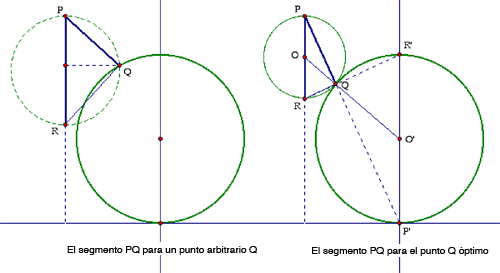
Supongamos que dos cuentas se sueltan simultáneamente desde el punto P, una cayendo por el segmento que une a P con Q y la otra cayendo verticalmente hacia R. La fuera de gravedad hace que las cuentas caigan la misma distancia, de manera que PQ = PR cos∠RPQ.  El punto Q al que se llega en el mínimo tiempo posible es aquel que corresponde a la posición más alta de R. Como el ángulo del triángulo PQR en el punto Q es recto, PR es el diámetro del circulo que inscribe a PQR.  Se sigue que la posición optima de Q es obtenida cuando tal círculo es tangente al círculo original (como se ve en la figura de la derecha). Sea P’el punto más bajo del círculo dado (donde toca a la línea del suelo).

Afirmación. El punto Q por donde el segmento PQ es óptimo está en la línea PP'.

La forma más sencilla de probar la afirmación es notar que la circunferencia que inscribe a ΔPQR (centrada en O) es una homotecia con respecto al punto Q del círculo dado que inscribe a ΔP'QR' (centrado en O').  Alternativamente, como los círculos son tangentes en Q, la línea OO' que une los centros debe pasar por Q.  Además, como PO || P'O', los ángulos alternados interiores ∠POQ y ∠P'O'Q deben ser iguales; los ángulos en P' y Q en el triángulo isósceles P'O'Q miden ambos 1/2(180^o - ∠P'O'Q') mientras que los ángulos en P y Q en el triángulo POQ son ambos 1/2(180^o - ∠POQ). En otras palabras, los cuatro ángulos son iguales; en particular, ∠PQO = ∠P'QO, de manera que Q debe estar en el segmento PP' como se afirmó.

Método Geométrico 2.  (Fondanaiche y McIntosh).

            Sea s = PQ la distancia recorrida por la cuenta, y h = PH su proyección en el vertical PH₁.  Como se ve en la figura, , Q₁ es el punto donde PQ vuelve a intersecar el círculo, y

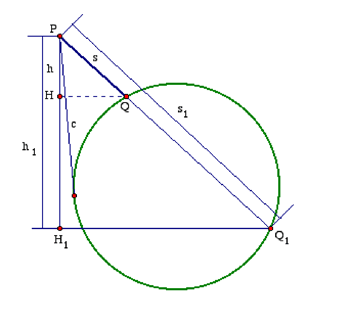
H₁ es la proyección de Q₁ en la vertical por P.  La ley de movimiento dice que la distancia s y el tiempo t requerido para recorrerla están relacionados mediante s = (1/2)at², o

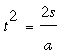
donde a = g cos ∠HPQ = g h/s es la aceleración debida a la gravedad a lo largo del segmento PQ.  Esto es,

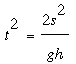
Para cualquier posición Q en el círculo, los triángulos PHQ y PH₁Q₁ son similares, de manera que s/h = s₁/h₁; también, un teorema básico de Euclides (III.36) dice que s·s₁ = c₂, done c es la longitud de la tangente desde P (que es constante).  Luego

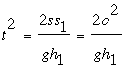
Esta última ecuación nos dice que t es inversamente proporcional a h₁ — el tiempo se minimiza cuando h₁ es máximo.  Debemos entonces elegir Q de manera que Q₁ sea el punto más bajo del círculo.

Otras soluciones.  Tanto Lim como Lian usaron cálculo para sus soluciones.  Resulta ser un agradable ejercicio, particularmente si uno hace como Lim y elige el origen como el punto más bajo del círculo. Tanto Robinson como Lian describieron Q en términos de coordenadas con el origen en el centro del círculo dado, lo que oscurece un poco su ubicación.