Solución del problema de Octubre, 2007

El problema:
	Un círculo de centro O y radio 1cm rueda por dentro de un triángulo cuyos lados miden 6cm, 8cm y 10cm, siempre tocando uno o más lados al rodar. ¿Qué distancia recorre O en un circuito completo?

Respuestas correctas:

El problema de este mes fue tomado de una lista de problemas de práctica para el 2002 Waterloo Mathematics Contests Seminar.  Recibimos soluciones correctas de Felix Arnaiz Lanzo 2  soluciones (España) Matthew Lim (USA) Gérard Billion (Francia) Jacques Mertzeisen (Francia) Ritwik Chaudhuri (India) Kacem Nouini (Francia) Sébastien Dumortier (Francia) Mark Pilloff (USA) Baptiste Gorin -- 2 soluciones (Francia) John T. Robinson (USA) Xavier Hecquet (Francia) K. Sengupta (India) Normand LaLiberté (Ontario) A. Teitelman (Israel) Farid Lian Martínez (España(?)) Philippe Fondanaiche (Francia)

La solución:

 Solución.  Todos los respondentes notaron que al rodar el círculo por el triángulo dado, digamos ABC, su centro O se mantiene a una distancia de un cm del lado a lo largo del cual se mueve. La trayectoria del centro es por tanto un triángulo, digamos A'B'C', cuyos lados son paralelos a los de ΔABC. El problema se reduce entonces a encontrar el radio de la dilación que lleva A a A', B a B', y C a C'. Varias elegantes ideas fueron usadas para determinar que el cociente es ½, de manera que la distancia recorrida por O es la mitad del perímetro de ΔABC, esto es 

½(6 + 8 + 10) = 12.

Exhibimos a continuación 4 de las soluciones. 

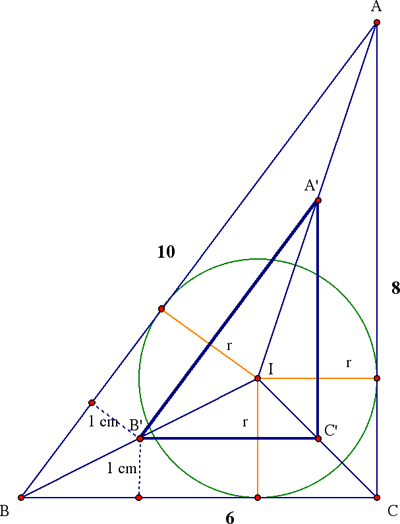
Método 1. El más popular. Como el vértice B’ del triángulo interior está a la misma distancia (1 cm) de los lados BC y BA tocados por el círculo cuando su centro está en el vértice B’, esto implica que yace sobre la bisectriz del ángulo correspondiente a B. Esto es válido para los tres vértices, de manera que

AA', BB', y CC' coinciden en el incentro I de ΔABC, que
es por tanto el centro de la dilación que lleva ΔABC a ΔA'B'C';           (1)
consecuentemente, I es también el incentro de ΔA'B'C'.

Buscamos el cociente de los inradios de los dos triángulos. Llamemos r al inradio de ΔABC. Como

(Area de ΔABC) = r · (semiperímetro) = r · ½(6 + 8 + 10 ) = 12r,

y el área es ½(6·8) = 24, deducimos que r = 2.  (Comentario. Area = r ·(semiperímetro) es un resultado standard que puede verse fácilmente en la figura de arriba, notando que el área del triángulo grande equivale a la suma de las áreas de los tres triángulos más pequeños tales como IBC que comparten el vértice I.)  Como el inradio de ΔA'B'C' es r – 1 = 1, la dilación que lleva ΔABC a ΔA'B'C' tiene razón ½, como dijimos. 

Comentario. Este método se aplica más generalmente a un círculo de radio r* rodando por un triángulo ABC cuyo semiperímetro es s u su area es F (con F obtenido con la fórmula de Herón); entonces r = F/s, y la razón de la dilación será (r – r*)/r.  Robinson lleva esta generalización un paso más allá, haciendo notar que el mismo argumento funciona para un polígono de n lados que tenga un círculo inscripto. Por supuesto, en el caso de un polígono arbitrario tanto el área como el perímetro tienen que ser dados.

Método 2 (Billion).  Como en el primer método, tenemos que encontrar r. Como 
BC² + CA² = 6² + 8² = 10² = AB²,

ΔABC tiene un ángulo recto en C.            (2)

El inradio de ΔABC puede obtenerse usando el hecho de que las tangentes desde un vértice hasta el círculo inscripto tienen igual longitud (ver figura). Como C es un ángulo recto,

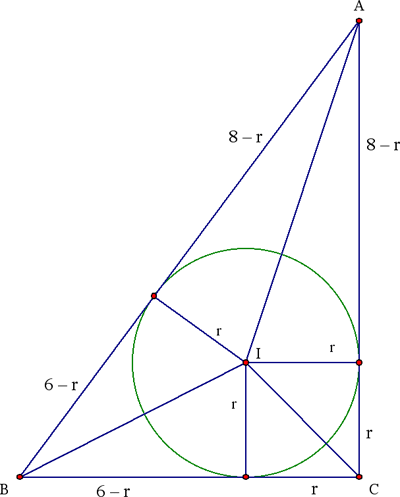
las tangentes desde C tienen longitud r.  Luego, perímetro = 6+8+10 = 24 es igual a
2·((6 – r) + r + (8 – r)) = 28 – 2r, de manera que nuevamente obtenemos r = 2.

Método 3.  Cinco de las soluciones recibidas usaron (1) junto con una fórmula trigonométrica como

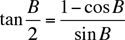
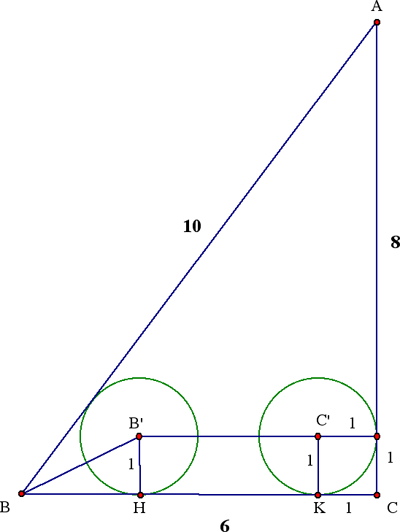
Como en la figura, cos B = 3/5 y sin B = 4/5, de donde tan (B/2) = 1/2.  Como
ΔBHB' = B/2 y B'H = 1, tenemos BH = 2.  Junto con BC = 6 y KC = 1, deducimos que HK  = 3.  Pero entonces B'C' = HK = 3, y vemos que el radio de la dilación deseado es
                                      B'C' : BC = 3 : 6 = 1:2.

Método 4. (Nouini, modificado para enfatizar la similitud con el método 3) Modificamos el método 3 usando similaridad de triángulos en lugar de trigonometría. Los triángulos congruentes S y T en la figura son similares a ΔABC; con un lado de 1 cm, la

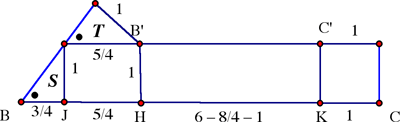
hipotenusa es 5/4 cm y el otro lado 3/4.  Entonces marcamos BJ como 3/4, JH como 5/4, y KC es 1; HK es entonces 6 – 2 – 1 = 3, como en el método 3.