Solución del problema de Septiembre, 2007

El problema:

Se disponen 6 puntos de manera tal que los 15 segmentos que los unen dos a dos tienen diferentes longitudes y apuntan en direcciones diferentes. Pruebe que uno de los segmentos es el lado más largo de uno de los triángulos formados y es, al mismo tiempo, el lado más corto de otro triángulo.   ¿Es verdadera la afirmación si comenzamos con 5 puntos (y los 10 segmentos que los unen siguen teniendo diferentes longitudes y diferentes direcciones)?

Respuestas correctas:
	Recibimos soluciones correctas de Philippe Fondanaiche (Francia), Wolfgang Kais (Alemania), John T. Robinson (USA), y K. Sengupta (India).

La solución:

  Los mayoría notó la relación de nuestro problema con el número de Ramsey R(3, 3).  Se puede encontrar una solución elemental en el lenguaje de la teoría de Ramsey en muchos libros.  John Robinson nos menciona soluciones particularmente elegantes en
http://www.cut-the-knot.org/Curriculum/Combinatorics/ThreeOrThree.shtml,
y
http://en.wikipedia.org/wiki/Ramsey's_theorem.
Tomamos nuestra version del problema de Mathematical Miniatures por Svetoslav Savchev y Titu Andreescu [publicado en 2003 por la Mathematical Association of America].

He aquí la solución de Kais, con algunas pequeñas modificaciones:
Las condiciones dadas aseguran que tres puntos cualesquiera forman un triángulo con un lado más corto, uno mediano y uno más largo. Es claro que los puntos y líneas pueden ser reemplazados por los 6 vértices y 15 lados de un grafo completo, con números diferentes asignados a cada lado, pero nos mantendremos en el lenguaje geométrico. Coloreemos un segmento rojo si es el lado más corto de un triángulo, y coloreemos el resto en azul. Como todo triángulo tiene un lado más corto, deducimos que

(*) no hay ningún triángulo azul.

Miremos uno de los puntos P y los cinco segmentos que lo conectan a los otros puntos. Como son o rojos o azules, sabemos que

(A) tres o más segmentos de P son rojos,

o

(B) tres o más segmentos de P son azules.

En cualquier caso, la configuración tiene un triángulo rojo: si vale (A), entonces los otros tres puntos finales de los segmentos rojos forman un triángulo con al menos un lado rojo (por *); este lado, justo con los lados rojos adyacentes conectados a P forman un triángulo rojo. Por otra parte, si se cumple (B), entonces (*) implica que ninguno de los segmentos que conectan dos de los tres otros puntos finales de los lados azules de P puede ser azul, de manera que tales segmentos forman un triángulo rojo. 
            El triángulo rojo encontrado es tal que cada segmento aparece como el lado más corto en al menos uno de los 20 triángulos de la configuración.  Por supuesto, este triángulo tiene un lado máximo que, al ser rojo, es también el lado más corto de algún triángulo.

Comentario. En el argumento no utilizamos la minimalidad de un lado más corto. Como cada triángulo tiene exactamente un lado más corto y uno más largo, el argumento puede ser fácilmente modificado para mostrar que al menos uno de los 20 triángulos consiste de tres lados tales que cada uno aparece como el lado más corto de algún triángulo, al menos uno de los triángulos consiste de tres lados que aparecen como medianos de otro triángulo, y al menos uno de los triángulos consiste de tres lados que aparecen como los más largos de otros triángulos.

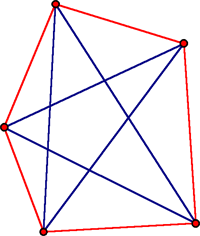
            Para ver que la afirmación no se cumple comenzando con 5 puntos, perturbemos los vertices de un pentágono regular de manera que los cinco lados y las cinco diagonales tengan diferentes longitudes. Esto se puede conseguir de manera que la más corta de las diagonales sea más larga que el más largo de los lados. En este caso cada conjunto de tres puntos forma un triángulo que tiene al menos una línea de cada tipo (dos lados y una diagonal, o dos diagonales y un lado). En ambos casos, el lado más corto de un triángulo no es nunca el lado más largo de otro triángulo.