Figure 1
En la Figura 1, ΔABC tiene lados de longitud s y un punto interior P. Una rotación de 60° sobre A lleva C a B y P a un
punto P'; luego, AP' = AP = 5, BP' = 13, y (como ΔAP'P es equilátero), P'P = 5. Se sigue que ΔBP'P tiene lados 5, 12, 13, de donde el ángulo en P es 90o. Se sigue que ∠BPA = 60o + 90o = 150o. El
Teorema del Coseno (con cos 150o = –√3/2) nos dice entonces que
s2 = AB2 = 52 + 122 – 2·5·12 cos 150o = 169 + 60√3.
El área de DABC es entonces
que es aproximadamente igual a 118.18.
Fondanaiche
evitó usa el Teorema del Coseno en su solución mediante el truco de extender BP hasta la base de la perpendicular desde A, llamada H en el diagrama de la derecha. ΔAPH es entonces un triángulo rectángulo con ángulos
de 30o y 60o, de manera que AH = 5/2 y PH = (5√3)/2;
obtenemos
como antes.
2 La solución de Collignon.
Figure 2
En esta solución rotamos P 60o en sentido horario alrededor de A para obtener C', alrededor de B para obtener A', y alrededor de C para obtener B'. Notemos que ΔAC'B ≅ ΔAPC, ΔBA'C ≅ ΔBPA, y ΔCB'A ≅ ΔCPB; esto nos dice que el área del hexágono AC'BA'CB' es exactamente el doble del área [ABC] que buscamos. El hexágono consiste de tres triángulos equiláteros (con
lados de longitud 5, 12, 13 respectivamente), y tres triángulos rectángulos
congruentes. Entonces,
2[ABC] = [AC'BA'CB']
=
[AC'P] + [BA'P] + [CB'P]
+ 3[PC'B]
y [ABC] =
169(√3/4) + 45.
3 La solución de Nadauld.En lugar de rotar el punto P, lo reflejamos en los lados AB para obtener C', BC para obtener A', y CA para obtener B'. Como
cada triángulo dentro de ΔABC que comparte el vértice P (por ejemplo
FIGURE 3
ΔAPB) es congruente con su imagen reflejada (es decir, ΔAC'B), el área [AC'BA'CB'] del hexágono exterior es el doble del
área [ABC] del
triángulo dado. Cada uno de los triángulos AC'B', BA'C', CB'A' es isósceles con el ángulo central de 120o; en efecto, cada uno se compone de un par
de triángulos rectángulos 30-60 con hipotenusas 5, 12, 13 respectivamente. Luego los lados opuestos a los ángulos
de 120° tienen longitudes B'C' = 5√3, C'A' = 12√3, y A'B' = 13√3, lo que implica que ∠A'C'B' = 90°. Se sigue que
2[ABC] = [AC'BA'CB']
=
[AC'B'] + [BA'C'] + [CB'A']
+ [A'B'C']
y [ABC] =
169(√3/4) + 45.
Solución 4. Esta solución fue usada por Visme,
Stadler, y Teitelman. Presentamos
aquí la solución de Stadler.
Sean α, β, γ los tres ángulos en P; específicamente, sea α = ∠BPC, β
= ∠CPA, γ= ∠APB. Sea s el lado
del triángulo. Entonces, por el Teorema del Coseno,
, 
y 
(*)
Como α + β + γ = 2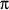
, tenemos 
; de donde 
y finalmente,
Insertando los
valores de (*) en esta ecuación obtenemos una ecuación de grado 6 en s:
s2(s4 - 338 s2 + 17761) = 0.
Esta ecuación
tiene soluciones y s2 =0, y s2 = 169 ± 60√3. Se verifica fácilmente que solamente s2 = 169 + 60√3 satisface α + β + γ = 2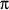. Este valor de s2 produce el valor
[ABC] =
169(√3/4) + 45 para el área del triángulo.
Comentarios. Varios lectores notaron que no hay nada
particular sobre el triángulo rectángulo de lados 5-12-13. Los mismos cuatro argumentos producirán
el área de DABC siempre que las distancias a, b, c desde P a los vértices satisfagan a2 + b2 = c2. Robinson generalizó más el problema; encontró el área [ABC] para cualquier punto P dentro del triángulo en función de las
distancias a = PA, b = PB, c = PC. De hecho, nuestra solución 3 (de Nadauld) nos da la respuesta
directamente: en lugar de encontrar el área de DA'B'C' usando propiedades de triángulos rectángulos,
podemos usar la fórmula de Herón y obtener
[ABC] = ½ [AC'BA'CB']
= ½ ([AC'B'] + [BA'C'] + [CB'A']
+ [A'B'C'])
Una consecuencia
notable de este argumento es que no importa donde se elija P dentro del triángulo equilátero, las
distancias a, b, c la
desigualdad triangular; en otras palabras, las distancias de P a los vértices no son arbitrarias, sino
que deben ser los lados de DA'B'C'. Dimitrie Pompeïu hizo esta observación en 1936. El Teorema de Pompeïu establece
que
Para cualquier punto P en el plano de DABC, las longitudes de los segmentos PA, PB, PC corresponden a los lados de
un triángulo a menos que P pertenezca el círculo suscripto por ΔABC, en cuyo caso las reflexiones de P en los lados, A', B', C', yacen en línea.
Sengupta
nos señaló la página de MathWorld
http://mathworld.wolfram.com/EquilateralTriangle.html
donde hay una
elegante formula de Martin Gardner (Mathematical Carnival: A New Round-Up of
Tantalizers and Puzzles from Scientific American, New York: Vintage Books, 1977, pp. 56-57, 63) para
el lado s de un
triángulo equilátero:
3(a4 + b4 + c4 + s4)=(a2 + b2 + c2 + s2 )2 ;
esta ecuación se
obtiene remplazando [ABC] con s2√3/4
en la ecuación de Robinson arriba y reordenando los términos. Richard
Guy reporta (en Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, 1994; especialmente la Sección D19, p. 183) que
una búsqueda por computadora mostró que a = 57, b = 65, c = 73, s = 112 es el menor ejemplo donde todos los parámetros
con enteros. Además, hay una familia infinita de soluciones enteras dada por
a = m2 + n2, b = m2 + mn + n2, c = m2 – mn + n2,
con m = 2(u2 + v2), n = u2 + 4uv + v2
y, entonces,
s = 8(u2 – v2)(u2 + uv + v2).
Nuestra modesta búsqueda encontró el problema discutido al menos dos veces
por Dr. Math:
http://mathforum.org/library/drmath/view/61863.html,
cuya fuente fue un problema Mensa de alrededor de 2002, y el item 55022 donde
hay una discusión de 1998. También
aparece como el problema 3682 en School Science and Mathematics de alrededor de 1975 (de acuerdo al Index
to Math Problems 1975-1979,
p. 135, de Stanley Rabinowitz). Véase
también Charles W. Trigg, Mathematical Quickies: 270 Stimulating Problems with Solutions. Dover (1985); publicado originalmente en 1967.
