|
Solución del problema de Marzo, 2009
| El problema: |
 |
Un poliedro de 6 aristas se llama tetraedro, y un poliedro de 8 aristas se llama piramide cuadrangular. Cómo se llama un poliedro de 7 aristas?
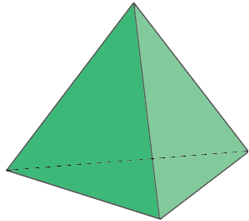
Tetrahedron
6 edges |
Quadrangular Pyramid
8 edges |
(consideramos un poliedro como una figura sólida con caras poligonales. Cada una de sus aristas une dos vértices y es la intersección de dos caras adyacentes. Un vértice es un punto donde se encuentran 3 o más lados, y forma una esquina en la que se encuentran tres o más caras.
|
Respuestas correctas: |
|
Recibimos soluciones correctas de
Bojan Basic (Serbia) |
Cornel Gruian (Rumania) |
Luigi Bernardini (Italia) |
Omran Kouba (Siria) |
Gérard Billion (Francia) |
Matthew Lim (USA) |
Lou Cairoli (USA) |
Catherine Nadault (Francia) |
Olivier Cyr (Francia) |
John T. Robinson (USA) |
Sébastien Dumortier (Francia) |
Albert Stadler (Suiza) |
Philippe Fondanaiche (Francia) |
A. Teitelman (Israel) |
Dereck Graefer (Regina) |
|
|
La solución:
Respuesta. El nombre podría ser inexistente: ningún poliedro puede tener exactamente 7 aristas. Este resultado es muy conocido, y Robinson encontró dos páginas web que lo discuten:
http://www.maths.usyd.edu.au/u/sandrab/math2009/t06sol.pdf (ver punto 5), y
http://plus.maths.org/issue43/features/kirk/proof.html.
Las respuestas recibidas muestran diversos argumentos; mostraremos tres de ellos, y después mostraremos que el número de aristas de un poliedro puede ser cualquier entero mayor que siete..
Notación. Denotaremos por v el número de vertices, f el número de caras, y e el número de aristas. El Teorema de Euler dice que para cualquier poliedro,
v – e + f = 2
Por ejemplo, para un tetraedro v = 4, f = 4, e = 6. Los primeros dos métodos utilizan el Teorema de Euler.
Método 1 (Billion y Dumortier).
Como cada lado une dos vertices y cada vértice recibe al menos tres aristas,
3v ≤ 2e.
Como queremos e = 7, se tiene que cumplir que v ≤ 14/3, y el único valor posible de v (un entero) es 4. Pero 4 vértices determinan a lo sumo
 aristas, lo que es una contradicción. Concluimos que e no puede ser 7.
Método 2 (Gruian, Kouba, Robinson).
Para que un poliedro tenga una cara con cuatro o más vértices, tiene que tener al menos 8 aristas: la cara tiene cuatro aristas y cada uno de los vértices se conecta a otro vértice fuera de la cara. Como queremos que haya solamente 7 aristas, todas las caras son triángulos; como cada cara tiene exactamente tres aristas mientras que cada lado pertenece a dos caras, 3f = 2 ´ 7, que carece de solución entera f.
Método 3 (el más popular).
Como un poliedro con 4 vértices tiene a lo sumo
aristas, cualquier poliedro de 7 aristas tiene al menos 5 vértices. De igual modo, con solamente 4 caras tendría a lo sumo 6 aristas, de manera que tiene que tener al menos 5 caras. Pero entonces tendríamos v + f ≥ 10, en contradicción con el Teorema de Euler's que con e = 7, nos da v + f = 9.
Comentarios. Obviamente un poliedro tiene al menos 4 vértices, de manera que tiene al menos 6 aristas. Ya probamos que el número de aristas no puede ser 7. Cairoli consideró la pregunta de si existen otros valores imposibles de e. La respuesta es no:
Hay un poliedro con exactamente e aristas para e = 6 y para e ≥ 8.
Una pirámide con base n-gonal tiene e = 2n aristas; esto hace posible cualquier par mayor o igual a 6. Podemos truncar esta pirámide y obtener un poliedro con un número impar de aristas si cortamos una de las esquinas de la base en forma de tetraedro: el vértices en la base de la pirámide queda remplazado por una cara triangular, dejando el poliedro con e = 2n + 3 aristas, lo que hace posible 9 y cualquier impar mayor. Una forma alternativa es apoyar un tetraedro en una de las caras triangulares de la pirámide. Esto agrega 3 lados, llevando el total a e = 2n + 3 aristas.
|
