|
Solución del problema de Noviembre, 2008
| El problema: |
 |
PM81: Noviembre 2008
¿Para qué k ≥ 3 es 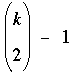 igual a pn, con p primo? igual a pn, con p primo?
|
Respuestas correctas: |
 |
Nuestro problema es el Problem 984 en Crux Mathematicorum with Mathematical Mayhem, 12:1 (Enero 1986), pp. 15-16 (en los días en que la revista se llamaba simplemente Crux Math). Recibimos soluciones de
Bojan Basic (Serbia) |
Farid Alberto Lian Martínez (Colombia) |
Gérad Billion (Francia) |
Matthew Lim (USA) |
Jean Braconnier (Francia) |
Sébastien Racanière (UK) |
Olivier Cyr (Francia) |
John T. Robinson (USA) |
Dan Dima (Rumania) |
Albert Stadler (Suiza) |
| Philippe Fondanaiche (Francia) |
Bernard Carpentier (Francia) |
| Catherine-A. Nadault (France) |
|
Sin embargo dos de nuestros lectores fueron un poco descuidados este mes y no prestaron atención a un par de casos: sus soluciones están incompletas.
|
La solución:
k puede tomar los valores 3, 4, 5, 8. Todas las soluciones recibidas utilizaron el mismo argumento. Sea 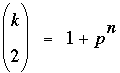 , con k, n enteros positivos, p primo. Entonces tenemos que , con k, n enteros positivos, p primo. Entonces tenemos que
(k – 2)(k + 1) = 2pn, (1)
de manera que (i) k – 2 es par; o (ii) k + 1 es par.
Caso (i). Si k – 2 = 2m, m ≥ 1, entonces (1) se convierte en m(2m + 3) = pn, lo que implica que m = pr , y
2pr + 3 = pn–r. (2)
- r = 0. Por (2) tenemos m = 1, 2m + 3 = 5 = pn; luego, k = 4, pn = 5.
- r ≥ 1. Ahora p debe dividir ambos miembros de (2), de manera que p divide a 3 y entonces p = 3. La ecuación (2) se convierte en 2·3r + 3 = 3n–r, de donde deducimos que 2·3r–1 + 1 = 3n-r–1. El lado derecho no puede ser 1 (porque eso implicaría que 2·3r–1 = 0); y entonces r – 1 = 0 (de otro modo el lado izquierdo sería
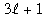 para algún entero no nulo para algún entero no nulo 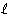 , y no sería divisible por 3). Concluimos que n = 3, m = 3, 2m + 3 = 9, o sea que en este subcaso k = 8, pn = 27. , y no sería divisible por 3). Concluimos que n = 3, m = 3, 2m + 3 = 9, o sea que en este subcaso k = 8, pn = 27.
Caso (ii). Sea k + 1 = 2m, m > 1. Entonces (1) es m(2m – 3) = pn, , que implica m = pr para algún r ≥ 1, y
2pr – 3 = pn–r. (3)
- n – r = 0. Por (3) tenemos r = n = 1, p = 2; luego, k = 3, pn = 2.
- n – r ≥ 1. Aplicando argumentos de divisibilidad a (3) obtenemos que p = 3, de manera que (3) se convierte en 2·3r–1 – 1 = 3n-r–1. Nuevamente 3r–1 o 3n-r–1debe ser 1. Aquí estas condiciones implican r = 1, n = 2, y entonces k = 5, pn = 9.
|