|
Solución del problema de abril, 2010
| El problema: |
 |
¿Qué puede decirse sobre los ángulos de un triángulo que tiene la propiedad de que si se divide la suma de los cubos de los lados por el perímetro, se obtiene el cuadrado de uno de los lados?
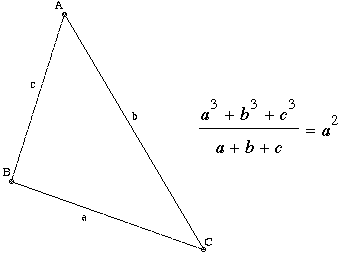
|
Respuestas correctas: |
 |
Bahman Ahmadi
(Regina) |
Sébastien Dumortier
(Francia) |
Remo Mantovanelli
(Italia) |
Halima Bashier
(Regina) |
Amit Elazari |
Milan Pavic
(Serbia) |
Bojan Basic
(Serbia) |
Mei-Hui Fang
(Austria) |
Arnaud Piquerez
(Francia) |
Luigi Bernardini
(Italia) |
Philippe Fondanaiche
(Francia) |
John T. Robinson
(USA) |
José Borges
(Portugal) |
Bruce Golfman
(Austria) |
Albert Stadler
(Suiza) |
Bernard Carpentier
(Francia) |
Cornel Gruian
(Rumania) |
A. Teitelman
(Israel) |
Bernard Collignon
(Francia) |
Benoît Humbert
(Francia) |
Jan van Delden
(Holanda) |
Andrew Cooke
(China) |
Magnus Jakobsson
(Suecia) |
Ray Van Raamsdonk
(British Columbia) |
Shai Covo
(Israel) |
Wolfgang Kais
(Alemania) |
Constantin Fishkin
(Ontario) |
Dan Dima
(Rumania) |
Normand LaLiberté
(Ontario) |
Benjamin Louradour
(Francia) |
Allen Druze
(USA) |
Farid Alberto Lian Martínez
(Colombia) |
 KURIHARA Tomohiro KURIHARA Tomohiro
(Japan)
|
También recibimos cinco soluciones incorrectas.
|
La solución:
Veremos que si etiquetamos el triángulo ΔABC de manera tal que el ángulo en el vértice A es opuesto al lado cuyo cuadrado se obtiene, entonces ∠A = 60°. Las medidas de los otros dos ángulos pueden ser cualquier par de números positivos tales que su suma es 120.
Comenzando con el cociente dado, tenemos
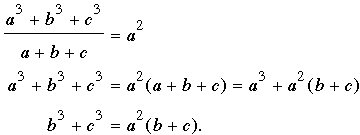
Como b3 + c3 = (b2 - bc + c2)(b + c) and b + c > 0 (porque por definición los lados de un triángulo son positivos), la última ecuación se convierte en
b2 - bc + c2 = a2.
Por el Teorema del Coseno, a2 = b2 + c2 - 2bc cos A, e igualando ambas expresiones para a2 nos da – bc = –2bc cos A, ó
cos A = 1/2.
Como los ángulos de un triángulo están entre 0° 180°, se tiene , ∠A = 60°. Como todos los pasos dados son reversibles, si ∠A = 60°, entonces 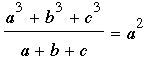
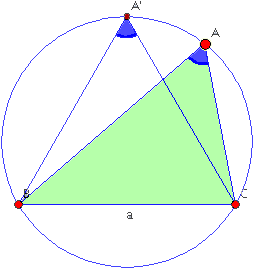
El triángulo A'BC en la figura es equilátero. Cliqueando en la figura se obtiene una aplicación java en la que el vértice A puede moverse a lo largo del arco superior BC del círculo; al moverse, obtenemos todos los triángulos con la propiedad mencionada en el problema que tienen a = BC como uno de sus lados. Durante su movimiento el ángulo A se mantiene fijo en 60°; aunque B y C varíen, siempre suman 120°. Similarmente, las longitudes de b y c varían al moverse A, pero el Teorema del Coseno implica b2 + c2 - 2bc cos A, y por tanto 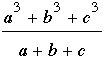 es constante e igual a a2. es constante e igual a a2.
|