|
Solución del problema de enero, 2009
| El problema: |
 |
Muestre que el producto
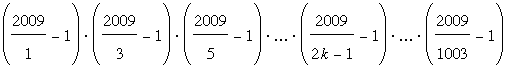
es una potencia de 2.
|
Respuestas correctas: |
 |
Recibimos soluciones correctas de
Berkay Anahtarci,
(Turquía) |
Philippe Fondanaiche
(Francia) |
Claude Morin
(Francia) |
Claudio Baiocchi,
(Italia) |
Tom Fuzesy
(Regina) |
Milan Pavic
(Serbia) |
Halima Bashier
(Regina) |
Bruce Golfman
(Austria) |
Shpetim Rexhepi
(Macedonia) |
Bojan Basic
(Serbia) |
Cornel Gruian
(Rumania) |
Eric Reynaud
(Francia) |
Luigi Bernardini
(Italia) |
David Jackrel
(USA) |
John T. Robinson
(USA) |
José Borges
(Portugal) |
Magnus Jakobsson
(Suecia) |
Heri Setiyawan
(Indonesia) |
Lou Cairoli
(USA) |
Wolfgang Kais
(Alemania) |
Nutheti Shivdeep
(India) |
John Campbell
(Alberta) |
Stephen La Rocque
(Ontario) |
A. Teitelman
(Israel) |
Bernard Carpentier
(Francia) |
Normand LaLiberté
(Ontario) |
Jan van Delden
(Holanda) |
Bernard Collignon
(Francia) |
Daniel Lu
(USA) |
Ray Van Raamsdonk
(British Columbia) |
Olivier Cyr
(Francia) |
Remo Mantovanelli
(Italia) |
Leonardo Vicchi
|
Mei-Hui Fang
(Austria) |
Patrick Gordon
(Francia) |
Allen Druze
(USA) |
| |
Karim Laaouini
(Marruecos) |
|
Comenzaremos con una demostración que fue común a muchas de las solucioens recibidas. Seguiremos con dos generalizaciones que tienen el mismo nivel de dificultad que el problema original, y terminaremos con otras dos generalizaciones.
|
La solución:
El problema original.
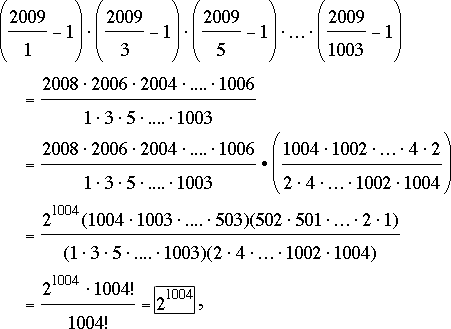
que es una potencia de 2.
Una generalización. Diez lectores observaron que el número 2009 puede remplazarse por 4n + 1; es decir, para todo entero n ≥ 1,
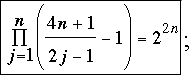 (1) (1)
el problema original era el caso n = 502. Bernardini, Colignon, Golfman, Gruian, Morin, y van Delden aplicaron una version del argumento dado arriba, es decir
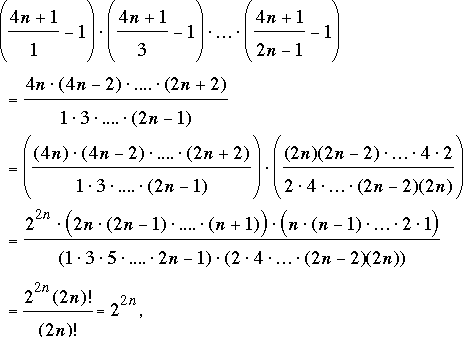
as claimed.
Inducción. Basic, Fondanaiche, y La Liberté, y Vicchi llamaron P(n) al producto del lado izquierdo en la ecuación (1), y usaron inducción para probar que P(n) = 22n. P(1) es simplemente 5 – 1 = 22; asumiendo que P(k) =
22k; debemos probar que P(k + 1) = 22(k+1).
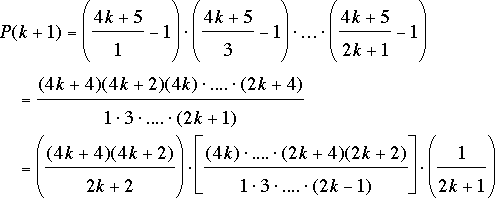
donde hemos insertado 2k + 2 tanto en el numerador como en el denominador. Notemos que la expresión entre corchetes es P(k), que estamos asumiendo es igual a 2k. Entonces,
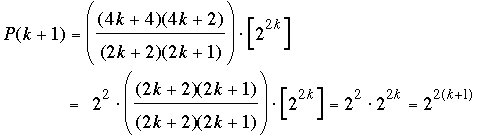
como se quería probar.
Comentarios. Agradecemos a nuestro colega Richard McIntosh por haber sugerido el problema de este mes. Richard descubrió la ecuación (1) y varias identidades similares investigando los números de Bernoulli y Euler. Una versión de (1) vale para 4n – 1, concretamente
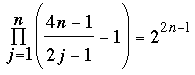 , n ≥ 1. (2) , n ≥ 1. (2)
Más aún, hay una identidad con un signo más en el producto:
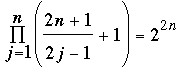 , n ≥ 1. (3) , n ≥ 1. (3)
Las identidades (2) y (3) pueden ser probadas usando los mismos métodos que funcionaron para probar (1).
|