|
Solución del problema de marzo, 2010
| El problema: |
 |
En el mes 3, ofrecemos un problema en tres partes.
Decida en cada caso si existen enteros s,t, mayores que 1, tales que:
- (ss)2 = tt?
- ( ss)2010 = tt?
- s(s2010) = tt?
|
Respuestas correctas: |
 |
Este problema proviene de el "Problem of the Week" número 1038 de Stan Wagon (Septiembre 26, 2005). Recibimos soluciones de
Bojan Basic (Serbia) |
Magnus Jakobsson (Suecia) |
Shai Covo (Israel) |
Wolfgang Kais (Alemania) |
Mei-Hui Fang (Austria) |
Matthew Lim (USA) |
Philippe Fondanaiche (Francia) |
John T. Robinson (USA) |
Cornel Gruian (Rumania) |
Jan van Delden (Holanada) |
Benoît Humbert |
Ray Van Raamsdonk |
Algunas de estas soluciones contenían afirmaciones no justificadas que llevaban a conclusiones erróneas. Dado que los argumentos eran esencialmente correctos, hemos incluido a los autores en la lista, pero recordamos a todos que en matemáticas uno debe estar seguro de que cada argumento es correcto y sostenido por un argumento válido.
|
La solución:
Parte a. No hay enteros s y t mayores que 1 tales que (ss)2 = tt.
Notemos que (ss)2 = s2s. Si hubiera un par s y t como el buscado, como s,t >1 tenemos ss < s2s = tt, lo que implica s < t; por otra parte, tt = s2s < (2s)(2s), de dondet < 2s. Pero t < 2s implica que st divide a s2s = tt, por lo que s divide a t; pero s < t < 2s implica que el menor múltiplo de s es mayor que t, es decir que s no dividir a t. La contradicción implica que tal par de números no puede existir.
Part b. Hay muchos pares posibles, por ejemplo,
|
and |
| s = 20092009 y t = 20092010. |
|
Para descubrir el primer par tenemos
(ss)2010 = s2010s = s2·1005s = (s2)1005s,
que tiene la forma ttsi ponemos s2 = 1005s; es decir, s = 1005.
Comentario. Este truco funciona para todos los exponentes pares salvo 2:
| para todo entero k > 1, (ss)2k = tt si s = k, t = k2. |
Por ejemplo si k = s = 2, t = 4: (22)4 = 28 = 44.
Para ver de dónde viene el segundo par mencionado arriba, notemos que
| para todo entero n > 2, (ss)n = tt si s = (n – 1)n–1, t = (n – 1)n. |
En el menor caso posible, n = 3, tenemos n = 3 we have s = 22 = 4, t = 23 = 8, y
(ss)3 = (22)3·22 = (23)2·22 = (23)(23); es decir, 412 = 88.
En nuestro problema n = 2010, s = 20092009, and t = 20092010:
(ss)2010 = (20092009)2010·20092009 = (20092010)2009·20092009
= (20092010)(20092010) = tt.
En general,
(ss)n = ((n-1)n-1)n·(n-1)n-1 = ((n-1)n)(n-1)·(n-1)n-1 = ((n-1)n)((n-1)n) = tt.
Comentario. Estamos ante un caso de lo que podríamos llamar un teorema anti-Fermat: no tiene solución entera cuando el exponente es 2, pero tiene muchas soluciones cuando el exponente es mayor a 2; además la demostración con seguridad entraría en el margen del libro de Fermat.
| Part c. Sí, hay un par que lo cumple: |
|
Tenemos
s(s2010) = ss·(s2009) = (ss)(s2009).
Para llevar esto a la forma tt, podemos hacer s = 2009. Similarmente,
| para todo n > 2, (ss)n = tt cuando s = n – 1 and, t = (n – 1)n. |
Por ejemplo, cuando n = 3, s = 2, t = 22 = 4 tenemos 2(23) = 44.
Observaciones.
Kais y Lim investigaron si es posible determinar todas las soluciones en los casos generales de las partes (b) y (c). Para la parte (b) fijamos un entero positivo n, y nos preguntamos qué pares de enteros s, t ≥ 2 satisfacen (ss)n = tt. Podemos obtener una solución parcial a la pregunta adoptando un argumento muy simple de Jakobsson (que solo lo aplicó al problema original). Como está claro que s y t deben ambos tener los mismos divisores primos, buscaremos las soluciones que se pueden escribir s = ak, t = am para un divisor común apropiado a y enteros k y m. Como (ss)n = tt vale si y solo si aknak = amam,
vale si y solo si knak = mam. Es decir, existen soluciones s y t que son potencias del mismo entero si y solo si existen k, m con m > k tales que
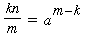 . .
Si m es cualquier divisor mayor que 1 del exponente n, hay una solución con
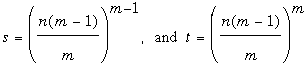
En particular, cuando m = n obtenemos la solución s = (n – 1)n–1, t = (n – 1)nque verificamos arriba. Cuando n tiene divisores propios tenemos otras opciones para m. El caso n = 2010, como 2010 = 2·3·5·67, hay 15 divisores m de n mayores que 1, todos los cuales generan una solución:
m |
2010 |
1005 |
670 |
402 |
335 |
201 |
134 |
67 |
n/m |
1 |
2 |
3 |
5 |
6 |
10 |
15 |
30 |
s |
20092009 |
20081004 |
2007669 |
2005401 |
2004334 |
2000200 |
1995133 |
198066 |
t |
20092010 |
20081005 |
2007670 |
2005402 |
2004335 |
2000201 |
1995134 |
198067 |
m |
30 |
15 |
10 |
6 |
5 |
3 |
2 |
n/m |
67 |
134 |
201 |
335 |
402 |
670 |
1005 |
s |
194329 |
187614 |
18099 |
16755 |
16084 |
13402 |
1005 |
t |
194330 |
187615 |
180910 |
16756 |
16085 |
13403 |
10052 |
Por ejemplo,
(194329)(194329)2010 = (194329)30·67·(194329) = (194330)29·67·(194329)
= (194330)1943·(194329) = (194330)(194330)
Kais usó su computadora para mostrar que cuando n = 2010 no hay otras soluciones aparte de las 15 mencionadas. Tanto él como Lim mostraron que para valores apropiados de n hay otras opciones. Por ejemplo, cuando n = 11 podemos tomar m = 11 y k= 8, k= 9 (además de nuestro canónico k = m – 1 = 10) :
Para n = 11, m = 11, k = 8, tenemos kn/m = 8 = a11–8 = a3; luego a = 2, s = 28, t = 211.
Para n = 11, m = 11, k = 9; tenemos kn/m = 9 = a11–9 = a2; luego a = 3, s = 39, t = 311.
Para n = 11, m = 11, k = 10; tenemos kn/m = 10 = a; luego s = 1010, t = 1011.
También en este caso la computadora de Kais mostró que para n = 11 no hay otras soluciones además de las mencionadas.
Para otras soluciones de (ss)n = tt, hacemos de nuevo s = ak and t = am. Esto implica
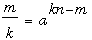
Para n > 2, la elección k = 1, m = n – 1, lleva a la solución a = n – 1; luego, s = n – 1, t = (n – 1)n–1. Kais probó que no hay solución para n = 2, y mostró (usando la computadora) que la elección k = 1 produce solución única cuando n = 2010 (la mencionada arriba). También aquí tenemos, para n = 11, tres soluciones en el caso k = 1, y ninguna para otros valores de k: parar m = 8 tenemos s = 2, t = 28; para m = 9 tenemos s = 2, t = 29; y para m = 10 tenemos s = 2, t = 210.
Finalmente notemos que, para n fijo, cualquier solución de (s)sn = ttgenera una solución de (SS)n = TT esto se logra poniendo S = t, T = sn: (SS)n = ( tt)n = (s(sn))n = sn(sn) = (sn)(sn) = TT. El truco no puede usarse en la dirección opuesta, ya que hemos visto que en general hay más soluciones en la parte (b) que en la parte (c).
|