|
Solución del problema de Diciembre, 2010
| El problema: |
 |
¿Es (20102011!)2 mayor que 2010201120102011?

|
Respuestas correctas: |
 |
Recibimos soluciones completas de
| Bojan Bašić (Serbia) |
Wolfgang Kais (Alemania) |
| Luigi Bernardini (Italy) |
Paul King (Ontario) |
| José Borges (Portugal) |
Normand LaLiberté (Ontario) |
| Lou Cairoli (USA) |
Matthew Lim (USA) |
| José David Calcines Padilla |
Remo Mantovanelli (Italy) |
| K.A. Chandrashekara (India) |
Nawal Kishor Mishra (India) |
| Bernard Collingnon (Francia) |
Vincent Pantaloni (Francia) |
| Gruian Cornel (Romania) |
Paolo Perfetti (Italy) |
| Shai Covo (Israel) |
Christian Pont (Francia) |
| Allen Druze (USA) |
Shpetim Rexhepi (Macedonia) |
| Mei-Hui Fang (Austria) |
John T. Robinson (USA) |
| Philippe Fondanaiche (Francia) |
Ilir Selmani (Macedonia) |
| Paul Führmann and Nicolas Michel (Francia) |
Heri Setiyawan (Indonesia) |
| Bruce Golfman (Austria) |
Madan Mohan Singhal |
| Verena Haider (Austria) |
Albert Stadler (Suiza) |
| Paul Hatfield (Australia) |
Todd Stohs |
| Benoît Humbert (Francia) |
Damian Straszak (Polonia) |
| Ile Ilijevski (Macedonia) |
A. Teitelman (Israel) |
| Kipp Johnson (USA) |
Paul Voyer (Francia) |
Recibimos dos respuestas incompletas.
|
La solución:
La respuesta es sí; ni siquiera están cerca. La computadora de Bašić determinó que (20102011!)2 tiene más de 276 × 106 dígitos, mientras que 2010201120102011 tiene menos de 147 × 106 dígitos — ¡casi la mitad! Robinson hace notar que ya cuando n = 3, (3!)2 > 33 (es decir, 36 > 27), y probó que (n!)2 crece más rápido que nn para n > 2. Recibimos una gran variedad de demostraciones, y hasta algunos lectores enviaron varios argumentos. El record corresponde a D. Kipp Johnson, que disfrutó tanto nuestro desafío que envió ¡siete pruebas! (sus palabras textuales fueron, “me han robado muchas horas de sueño con este problema”) Presentaremos cuatro de sus pruebas, suplementando su trabajo con una quinta prueba de Singhal y Golfman, más algunas buenas ideas de los demás lectores. El premio a la simplicidad corresponde a la primera prueba, mientras que el premio a la originalidad va para la quinta.
Prueba #1 Una desigualdad elemental.
Primero notamos que para 1 ≤ k ≤ n,
k · (n - (k - 1)) = n + (k - 1)(n - k) ≥ n,
con igualdad si k = 1 ó k = n, y desigualdad estricta cuando 1 < k < n. Luego, para todo entero n > 2,
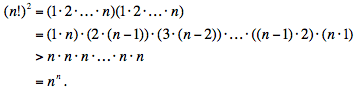
Proof # 2 Induction.
Queremos proba que (n!)2 > nn for n ≥ 3.
Tenemos (3!)2 = 36 and 33 = 27; luego (n!)2 > nn si n = 3. Este es el caso base. Ahora supongamos la afirmación para n = k; es decir, (k!)2 > kk para un cierto k ≥ 3. Se cumple (y lo probaremos en el párrafo siguiente) que 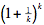 < 3 para todo entero positivo k, de donde deducimos que k + 1 > < 3 para todo entero positivo k, de donde deducimos que k + 1 > 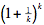 for k ≥ 2. si k ≥ 2. Entonces for k ≥ 2. si k ≥ 2. Entonces

Esto completa el paso inductivo, y concluimos que la hipótesis vale para todo ; en particular, vale para n = 20102011.
Comentario. Como 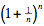 crece hacia el número e = 2.718... cuando , esta sucesión juega un rol importante en el análisis matemático. Pero no hace falta usar análisis para probar que crece hacia el número e = 2.718... cuando , esta sucesión juega un rol importante en el análisis matemático. Pero no hace falta usar análisis para probar que 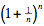 < 3; mostramos aquí un argumento simple que recibimos de Verena Haider, basado en el Teorema del Binomio: < 3; mostramos aquí un argumento simple que recibimos de Verena Haider, basado en el Teorema del Binomio:
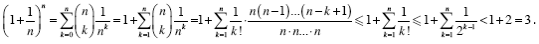
Prueba #3 Aproximación de Stirling.
La fórmula de Stirling para implica que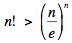 para todo entero positivo n. Cuando n ≥ 8 tenemos n > e2 , entonces para todo entero positivo n. Cuando n ≥ 8 tenemos n > e2 , entonces
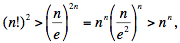
que muestra que (20102011!)2 > 2010201120102011.
Prueba #4 Sumas de Riemann. (Usamos aquí la versión de Matthew Lim)
Si n > e2, entonces ln n -2 > 0 y
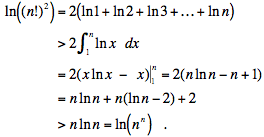
Finalmente, si exponenciamos ambos lados de la ecuación, obtenemos (n!)2 > nn para todo entero n ≥ 8.
Comentario. Esta prueba es esencialmente la misma prueba que la #3, salvo que hemos probado la fórmula de Stirling en lugar de usarla.
Agregamos aquí una idea que parece habérsele escapado a Johnson. Recibimos esta prueba de Madan Mohan Singhal; Bruce Golfman envió una prueba similar.
Preuba #5 La media aritmético-geométrica.
La sucesión
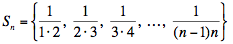
tiene n – 1 términos, que son distintos cuando n > 2. Su media aritmética es
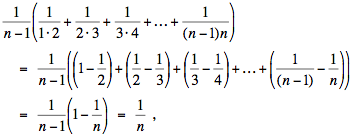
y su media geométrica es
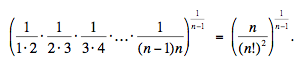
Como para sucesiones de números distintos la media aritmética es siempre mayor que la media geométrica, deducimos que para n > 2,
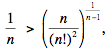
ó
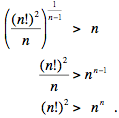
|