Solución del problema de Abril, 2013

El problema:
	Encuentre todos los pares $c$ y $d$ de números reales tales que todas las raíces de los polinomios $$6x^2-24x-4c \quad \mbox{ y } \quad x^3 +cx^2 +dx - 8$$ son números reales no-negativos.

Respuestas correctas:

Respuesta. Existe un único par de valores para los que todas las raíces son reales y no-negativas; éstos son $c = -6, d=12$. Recibimos soluciones correctas de Lamis Alsheikh (Siria) Diana Andrei (Suecia) Jose Arraiz (Francia) Ricardo Bernabé Baloni (Argentina) Aleksandar Blazhevski (Macedonia) Radouan Boukharfane (Québec) Lou Cairoli (USA) Bernard Carpentier (Francia) Allen Druze (USA) Edgardo Figueroa Donayre Jan Fricke (Alemania) Georges Ghosn (Québec) Tony Harrison (UK) Kipp Johnson (USA) Matthew Lim (USA) Patrick J. LoPresti (USA) Nawal Kishor Mishra (India) Luis Rivera Albert Stadler (Suiza) Bruno Tisserand (Francia)   También recibimos tres soluciones incompletas y una incorrecta.

La solución:

Cuando $c=-6, d=12$ los polinomios son $6(x-2)^2$ y $(x-2)^3$, de manera que las seis raíces son todas $x=2$, obviamente reales y no-negativas. Debemos entonces mostrar que no hay otros pares satisfactorios. El primer paso en todas las respuestas fue considerar la función cuadrática $f(x) := 6x^2-24x-4c$ y mostrar que para que sus raíces sean reales se debe tener $c \ge -6$: para esto, se puede notar que el discriminante es $24^2-4\cdot 6 \cdot (-4c) = 96(6+c)$, que es no-negativo precisamente cuando $c \ge -6$; o se puede escribir $f(x) = 6(x-2)^2 -4(c+6)$ y notar que su mínimo es $-4(c+6)$ en $x=2$, que está debajo del eje $x$ cuando $c \ge -6$. (el requerimiento de que las raíces de $f(x)$ fueran no-negativas no es necesario: esta condición fuerza $c \le 0$, pero veremos enseguida que la cúbica dada es mucho más restrictiva.)

Para analizar la cúbica se puede elegir entre utilizar cálculo o la desigualdad de la media aritmético-geométrica.

La desigualdad. Si $r,s,t$ son las raíces de la cúbica, tenemos
$$g(x) := x^3 +cx^2 +dx - 8 = (x-r)(x-s)(x-t).$$
Comparando coeficientes obtenemos $r+s+t = -c$, $rst = 8$. Para aplicar la desigualdad de la media aritmético-geométrica debemos usar el requisito de que las raíces son no-negativas; de hecho, son positivas (porque su producto es 8). La desigualdad nos dice que tres números positivos $r,s,t$ satisfacen
$$r+s+t \ge 3\sqrt[3]{rst},$$
de donde$-c \ge 6$; es decir, $c \le -6$. Pero habíamos determinado previamente que $c\ge -6$, de manera que $c = -6$. Se sigue que $r+s+t = 6 = 3\sqrt[3]{rst}$; entonces $r=s=t=2$, $d=12$. En consecuencia, $c = -6, d=12$ es el único par que satisface las condiciones.

Un argumento con cálculo. Todas las respuestas que evitaron la media aritmético-geométrica usaron cálculo de una u otra manera. Veamos el argumento de Harrison. Como la derivada segunda es
$g''(x) = 6x+2c$, la curva $y=g(x) = x^3 +cx^2 +dx - 8$ tiene un punto de inflexión en $\left(-\frac13c, \; \frac2{27}c^3-\frac13cd-8\right)$ (donde la derivada segunda es cero). Como $g'\left(-\frac13c\right) = d-\frac13c^2$, la tangente a la curva en el punto de inflexión tiene ecuación
$$y-\left(\frac2{27}c^3-\frac13cd-8\right) = \left(d-\frac13c^2\right)\left(x+\frac13c\right),
\quad \mbox{ ó } $$ $$\quad y= \left(d-\frac13c^2\right)x -\left(\frac1{27}c^3 + 8\right); $$
de manera que intersecta el eje $y$ cuando $y=-\left(\frac1{27}c^3 + 8\right)$. Como sabemos que $c \ge -6$, deducimos que la intersección con el eje $y$ es a lo sumo $\left(\frac1{27}(-6)^3 + 8\right) = 0$. Pero sabemos que para que nuestra cúbica tenga raíces distintas, debe de alcanzar su máximo relativo para algún valor de $x$ entre 0 y el punto de inflexión, como se ve en el diagrama. Además, este máximo debe estar debajo de la línea que es tangente a la curva en el punto de inflexión; pero sabemos que esta tangente tiene que tener pendiente negativa y está debajo del eje $x$, de manera que la curva no puede tocar la parte positiva del eje $x$ a la izquierda del punto de inflexión. La conclusión es que la tangente en el punto de inflexión coincide con el eje $x$; esto fuerza$\frac1{27}c^3 + 8 = 0$ y, en conclusión, $c=-6$. Finalmenten la pendiente de la tangente, $d-\frac13c^2$, debe ser 0, por lo que $d = 12$, como se quería.

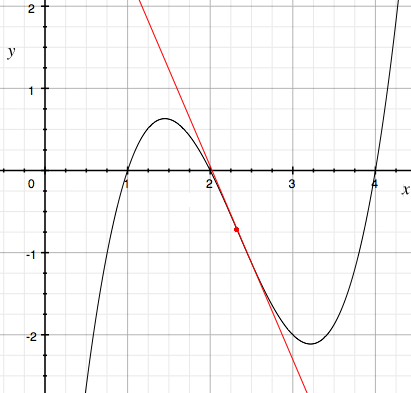
El gráfico de la cúbica con raíces distintas,
junto con su tangente en el punto de inflexión.

Fuente. Nuestro problema de abril fue el número 4 en la competencia de selección de la olimpíada matemática de Estonia en 2004-2005. Ver Crux Mathematicorum 35:1 (Febrero 2009) pág. 28.