|
Solución del problema de Septiembre, 2012
| El problema: |
 |
$N$ es un conjunto que contiene algunos números naturales entre 1 y 15, y tiene la propiedad de que el producto de tres cualquiera de sus miembros no es un cuadrado. Por ejemplo, si $N$ contuviera 2 y 6, no puede contener a 12 porque $2\cdot 6 \cdot 12 = 144$, que es un cuadrado. ¿Qué tan grande puede ser $N$? |
Respuestas correctas: |
 |
$N$ puede contener a lo sumo 10 números.
Recibimos soluciones correctas de
| Lamis Alsheikh (Siria) |
Aleksandar Blazhevski (Macedonia) |
| Lou Cairoli (USA) |
Bernard Collignon (Francia) |
| Mei-Hui Fang (Austria) |
Philippe Fondanaiche (Francia) |
| Tom Fuzesy (Regina) |
Matthew Lim (USA) |
| Matthew Lim (USA) |
Albert Stadler (Suiza) |
| Hakan Summakoğlu (Turkey) |
Arthur Vause (Reino Unido) |
También recibimos tres respuestas incorrectas. |
La solución:
El problema de este mes fue uno de los problemas de teoría de números que llegó a la
lista final para la 35$^{\rm a}$ Olimpíada Matematica Internacional, llevada a cabo en
Hong Kong en 1994. Aunque el problema tiene una solución corta y elegante, lleva mucho tiempo encontrar una solución satisfactoria, y
muchos intentos promisorios tienden a fracasar; tal vez fue esto lo que hizo que el problema no fuera considerado para la olimpíada. De hecho, la mayoría
de las respuestas omitieron detalles o utilizaron una computadora. Solamente tres soluciones estaban completas. Presentamos aquí la solución de Lim,
que es directa y fácil de entender, aunque require mucho trabajo. Luego mostramos la solución de Summakoğlu,
que es elegante pero carece de motivación si uno no vio primero el argumento de Lim. La solución de Fang es también muy buena; es similar
a la solución del comité olímpico que puede encontrarse en sitios web como
http://mks.mff.cuni.cz/kalva/short/soln/sh94n1.html.
Solución de Lim con contribuciones de otros.
El conjunto $S$ de los enteros de 1 a 15 contiene $15 \choose 3$ $= 455$ subconjuntos de 3 elementos;
de estos, solamente 18 consisten de tres enteros cuyo producto es un cuadrado. Los llamaremos ternas cuadradas.
Es sencillo hacer una lista de las ternas cuadradas:
| {1,2,8} |
{2,3,6} |
{3,4,12} |
{5,8,10} |
| {1,3,12} |
{2,4,8} |
{3,5,15} |
{5,12,15} |
| {1,4,9} |
{2,5,10} |
{3,6,8} |
{6,8,12} |
| |
{2,6,12} |
{3,9,12} |
{6,10,15} |
| |
{2,7,14} |
|
{7,8,14} |
| |
{2,8,9} |
|
|
Nuestra tarea es encontrar $N\subset S$, lo más grande posible, tal que ningún subconjunto de $N$ está en la lista de ternas cuadradas. Equivalentemente,
buscamos un subconjunto de números a quitar de $N$ lo más {\em pequeÒo} posible pero que interseque cada terna cuadrada. Es fácil comprobar que
$X = \{1,2,8,12,15\}$ es un conjunto de 5 elementos que intersecta a todas las ternas; su complemento
$S-X = \{3,4,5,6,7,9,10,11,13,14\}$ es por tanto un subconjunto de 10 elementos de $S$ con la propiedad deseada.
Pero, øpuede haber un subconjunto de 11 elementos con tal propiedadú En otras palabras, øexiste un conjunto de 4 elementos que intersectaú
Antes de responder esta pregunta, veamos la lista de los seis conjuntos de 5 elementos que intersectan (la lista ha sido verifica con computadora por
varios lectores). Se puede chequear a mano que cada uno de estos conjuntos contiene al menos un número en la lista de ternas cuadradas.
| {1,2,3,8,15} |
{1,2,8,12,15} |
{2,3,4,8,15} |
| {2,3,8,9,15} |
{2,4,8,12,15} |
{2,8,9,12,15} |
Se sigue que hay seis conjuntos de 10 elementos en $S$ que sirven como candidatos
para ser el $N$ más grande.
Veamos que cualquier conjunto que intersecta tiene al menos 5 elementos. Consideremos las siguientes cuatro ternas disjuntas:
$$\{1,4,9\}, \{2,3,6\}, \{5,12,15\}, \{7,8,14\}.$$
Como son disjuntas, podemos estar seguros de que cualquier conjunto que interseque contendrá al menos un número de cada uno de estos cuatro conjuntos.
Esto implica de inmediato que $N$ no puede contener más que 11 elementos. Tratemos de construir $N$ removiendo 1 del primer conjunto, 3 del segundo, 5 del tercero,
7 del cuarto. En ese caso la terna $\{2, 4, 8\}$ aún sería un subconjunto de $N$, de manera que el conjunto de 11 elementos
no tendría la propiedad buscada. Ahora, hay $3^4 = 81$ maneras de remover un único número de cada una de las ternas; a menos que encontremos un atajo,
deberemos encontrar, para cada una de las 81 posibilidades,
una terna cuadrada que siga en $N$ después de que esos cuatro números fueron removidos. Así que sírvase un trago, prenda la TV, siéntese y relájese,
y haga una lista de las 81 maneras de elegir cuatro elementos, y encuentre en cada caso la terna cuadrado que no fue intersectada. Por suerte para nosotros,
Lim hizo el esfuerzo:
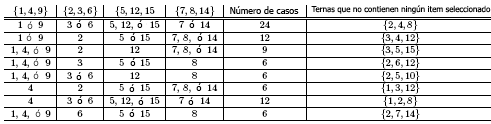
Entonces, para excluir todas las ternas cuadradas $N$ debe excluir más de 4 números de $S$. Como ya tenemos un ejemplo donde $N$ tiene 10 números, vemos que el
temaño máximo de $N$ es 10.
Solución de Summakoğlu. Probamos que $N$ no puede tener más que 10 elementos mostrando que todo conjunto que intersecta todas las ternas cuadradas
tiene al menos 5 elementos. Veremos que lcanza con determinar si 2 ó 3 están o no en el conjunto que intersecta. Hay que considerar tres posibilidades:
(i) tanto 2 como 3 están en el conjunto que intersecta (y por tanto no en $N$);
(ii) 2 está en el conjunto que intersecta y 3 está en $N$; (iii) 2 está en $N$.
Caso ($i$). $2\not\in N$, $3\not\in N$.
Como las ternas cuadradas $\{1,4,9\}, \{5,12,15\}$, $\{7,8,14\}$ son disjuntas, al menos un número de cada una debe ser omitido
de $N$; entonces el conjunto que intersecta resultante
tiene al menos 5 elementos.
Caso ($ii$). $2\not\in N$, $3\in N$.
Como $3 \in N$, al menos un número de $\{5, 15\}$ y $\{6,8\}$ debe ser omitido de $N$; además, como
$\{3,1,12\}, \{3,4,12\}, \{3,9,12\}$ y $\{1,4,9\}$ son ternas cuadradas, o se omite 12 junto con uno de 1, 4, 9, o tenemos que
3 y 12 están en $N$ de manera que 1, 4 y 9 deben ser omitidos. En cualquier caso, el conjunto que intersecta tiene al menos 5 elementos.
Caso ($iii$). $2\in N$.
Como $2 \in N$, al menos un número de cada uno de $\{3, 6\}, \{5,10\}$ y $\{7,14\}$ debe ser omitido de $N$;
además, como $\{2,1,8\}, \{2,4,8\}, \{2,9,8\}$ y $\{1,4,9\}$ son ternas cuadradas, o se omite 8 junto con uno de 1, 4, 9,
o tenemos 2 y 8 en $N$ de manera que 1, 4, y 9 deben ser omitidos. En cualquier caso, el conjunto que intersecta debe tener al menos 5 elementos.
|